
分析 (1)根据“奇异数”的定义,只需看能否把2k+2和2k这两个数写成两个连续偶数的平方差即可判断;
(2)运用平方差公式进行计算,进而判断即可;
(3)运用平方差公式进行计算,进而判断即可.
解答 解:(1)由题意得:(2k+2)2-(2k)2=4(2k+1),
所以奇异数一定是4的倍数;
(2)说法正确.4的偶数倍不是奇异数,如16=42-02不是奇异数;
(3)①m=8;
故答案为:8;
②是,
故答案为:是;
③不存在.因为奇异数一定是4的奇数倍,而美丽数是8的倍数,即是4的偶数倍,所以不存在既是奇异数又是美丽数的数.
点评 此题主要考查了平方差公式的应用,此题是一道新定义题目,熟练记忆平方差公式是解题关键.


科目:初中数学 来源: 题型:解答题
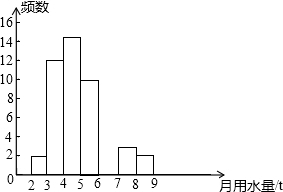 小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).| 月均用水量(单位:t) | 频数 | 百分比 |
| 2≤x<3 | 2 | 4% |
| 3≤x<4 | 12 | 24% |
| 4≤x<5 | 15 | 30% |
| 5≤x<6 | 10 | 20% |
| 6≤x<7 | 6 | 12% |
| 7≤x<8 | 3 | 6% |
| 8≤x<9 | 2 | 4% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2sinαcosα | B. | sinα | C. | cosα | D. | cos2α |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
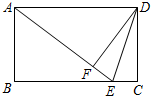 如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=3,BE:EC=4:1,则线段DE的长为$\sqrt{10}$.
如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=3,BE:EC=4:1,则线段DE的长为$\sqrt{10}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com