
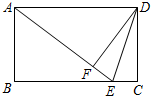
 如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=3,BE:EC=4:1,则线段DE的长为$\sqrt{10}$.
如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=3,BE:EC=4:1,则线段DE的长为$\sqrt{10}$. 分析 由翻折易得△DFE≌△DCE,则DF=DC,∠DFE=∠C=90°,再由AD∥BC得∠DAF=∠AEB,根据AAS证出△ABE≌△DFA;则AE=AD,设CE=x,从而表示出BE,AE,再由勾股定理,求得DE.
解答 证明:由矩形ABCD,得∠B=∠C=90°,CD=AB,AD=BC,AD∥BC.
由△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处,得△DFE≌△DCE,
∴DF=DC,∠DFE=∠C=90°,
∴DF=AB,∠AFD=90°,
∴∠AFD=∠B,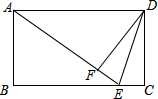
由AD∥BC得∠DAF=∠AEB,
∴在△ABE与△DFA中,
$\left\{\begin{array}{l}{∠AEB=∠DAF}\\{∠B=∠AFD}\\{AB=DF}\end{array}\right.$,
∴△ABE≌△DFA(AAS).
∵由EC:BE=1:4,
∴设CE=x,BE=4x,则AD=BC=5x,
由△ABE≌△DFA,得AF=BE=4x,
在Rt△ADF中,由勾股定理可得DF=3x,
又∵DF=CD=AB=3
∴x=1
在Rt△DCE中,DE=$\sqrt{E{C}^{2}+D{C}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$.
故答案是:$\sqrt{10}$.
点评 本题考查了三角形的全等和勾股定理的应用,一定要熟练掌握全等三角形的判定方法和勾股定理的内容.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
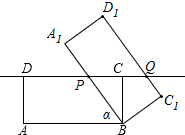 已知矩形ABCD,AB=8,BC=4,将它绕着点B按顺时针方向旋转α度(0<α≤180)得到矩形A1BC1D1,此时A1B,C1D1这两边所在的直线分别与CD边所在的直线相交于点P、Q,当DP:DQ=1:2时,DP的长为5或1+$\sqrt{11}$.
已知矩形ABCD,AB=8,BC=4,将它绕着点B按顺时针方向旋转α度(0<α≤180)得到矩形A1BC1D1,此时A1B,C1D1这两边所在的直线分别与CD边所在的直线相交于点P、Q,当DP:DQ=1:2时,DP的长为5或1+$\sqrt{11}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 计算日期 | 上期示度 | 本期示度 | 电量 | 金额(元) |
| 20110710 | 3 230 | 3 296 | 66 | 34.98 |
| 20110810 | 3 296 | 3 535 | 239 | 135.07 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
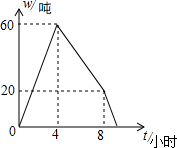 某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出物资的速度均保持不变).该仓库库存物资w(吨)与时间t(小时)之间的关系如图所示,求这批物资从开始调进到全部调出所需要的时间.
某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出物资的速度均保持不变).该仓库库存物资w(吨)与时间t(小时)之间的关系如图所示,求这批物资从开始调进到全部调出所需要的时间.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
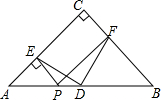 △ABC中,∠C=90°,BC=AC,D为AB中点,P是AB上一点,PE⊥AC于E,PF⊥BC于F.
△ABC中,∠C=90°,BC=AC,D为AB中点,P是AB上一点,PE⊥AC于E,PF⊥BC于F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
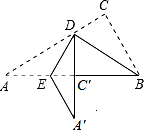 如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠,使点A落在DC′的延长线上的点A′处.若图中∠C=90°,∠A=30°,BC=5cm,则折痕DE的长为( )
如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠,使点A落在DC′的延长线上的点A′处.若图中∠C=90°,∠A=30°,BC=5cm,则折痕DE的长为( )| A. | 3cm | B. | $2\sqrt{3}$cm | C. | $2\sqrt{5}$cm | D. | $\frac{10}{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
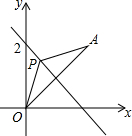 如图,平面直角坐标系中,A点坐标为(2,2),点P(m,n)在直线y=-x+2上运动,设△APO的面积为S,则下面能够反映S与m的函数关系的图象是( )
如图,平面直角坐标系中,A点坐标为(2,2),点P(m,n)在直线y=-x+2上运动,设△APO的面积为S,则下面能够反映S与m的函数关系的图象是( )| A. | 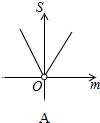 | B. | 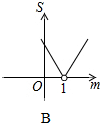 | C. | 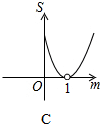 | D. | 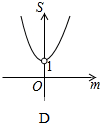 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com