Question

小明在学习三角形知识时，发现如下三个有趣的结论：在Rt△ABC中，∠A=90°，BD平分∠ABC，M为直线AC上一点，ME⊥BC，垂足为E，∠AME的平分线交直线AB于点F．

（1）M为边AC上一点，则BD、MF的位置是______．请你进行证明．
（2）M为边AC反向延长线上一点，则BD、MF的位置关系是______．请你进行证明．
（3）M为边AC延长线上一点，猜想BD、MF的位置关系是______．请你进行证明．

Answer 1

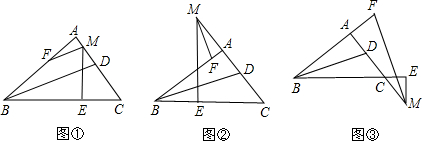
解：（1）BD∥MF．
理由如下：∵∠A=90°，ME⊥BC，
∴∠ABC+∠AME=360°-90°×2=180°，
∵BD平分∠ABC，MF平分∠AME，
∴∠ABD=∠ABC，∠AMF=∠AME，
∴∠ABD+∠AMF=（∠ABC+∠AME）=90°，
又∵∠AFM+∠AMF=90°，
∴∠ABD=∠AFM，
∴BD∥MF；

（2）BD⊥MF．
理由如下：∵∠A=90°，ME⊥BC，
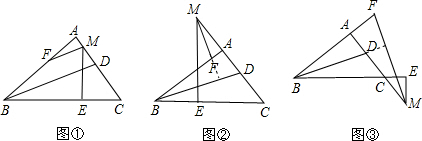
∴∠ABC+∠C=∠AME+∠C=90°，
∴∠ABC=∠AME，
∵BD平分∠ABC，MF平分∠AME，
∴∠ABD=∠AMF，
∵∠ABD+∠ADB=90°，
∴∠AMF+∠ADB=90°，
∴BD⊥MF；

（3）BD⊥MF．
理由如下：∵∠A=90°，ME⊥BC，
∴∠ABC+∠ACB=∠AME+∠ACB=90°，
∴∠ABC=∠AME，
∵BD平分∠ABC，MF平分∠AME，
∴∠ABD=∠AMF，
∵∠AMF+∠F=90°，
∴∠ABD+∠F=90°，
∴BD⊥MF．
分析：（1）根据角平分线的定义与四边形的内角和定理求出∠ABD+∠AMF=90°，又∠AFM+∠AMF=90°，然后证明得到∠ABD=∠AFM，然后根据同位角相等，两直线平行可得BD∥MF；
（2）先证明∠ABC=∠AME，再根据角平分线的定义可得∠ABD=∠AMF，然后根据∠ABD+∠ADB=90°得到∠AMF+∠ADB=90°，从而得到BD⊥MF；
（3）先证明∠ABC=∠AME，再根据角平分线的定义可得∠ABD=∠AMF，然后根据∠AMF+∠F=90°得到∠ABD+∠F=90°，从而得到BD⊥MF．
点评：本题考查了直角三角形的性质，垂线的定义，平行线的判定，三角形的内角和定理，本题规律性较强，准确识图，准确找出角度之间的关系是解题的关键．