
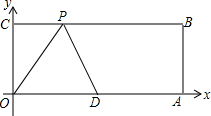
 如图,O为坐标原点,四边形OABC为长方形,边OA和OC分别落在x轴和y轴的正半轴上,且A(10,0),C(0,4),点D是OA的中点,点P在线段BC上运动,当△ODP为腰长为5的等腰三角形时,求点P的坐标.
如图,O为坐标原点,四边形OABC为长方形,边OA和OC分别落在x轴和y轴的正半轴上,且A(10,0),C(0,4),点D是OA的中点,点P在线段BC上运动,当△ODP为腰长为5的等腰三角形时,求点P的坐标. 分析 题中没有指明△ODP的腰长与底分别是哪个边,故应该分别从OD、OP与PD是底边去分析求解,从而求得点P的坐标.
解答 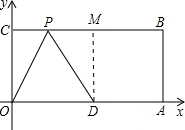 解:∵A(10,0),C(0,4),
解:∵A(10,0),C(0,4),
∴OC=4,OA=10,
∵点D是OA的中点,
∴OD=5,
(1)OD是等腰三角形的底边时,P就是OD的垂直平分线与CB的交点,此时OP=PD≠5;
(2)OD是等腰三角形的一条腰时:
①若点O是顶角顶点时,P点就是以点O为圆心,以5为半径的弧与CB的交点,
在直角△OPC中,CP=$\sqrt{O{P}^{2}-O{C}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,则P的坐标是(3,4).
②若D是顶角顶点时,P点就是以点D为圆心,以5为半径的弧与CB的交点,
过D作DM⊥BC于点M,
在直角△PDM中,PM=$\sqrt{P{D}^{2}-D{M}^{2}}$=3,
当P在M的左边时,CP=5-3=2,则P的坐标是(2,4);
当P在M的右侧时,CP=5+3=8,则P的坐标是(8,4).
故P的坐标为:(3,4)或(2,4)或(8,4).
点评 此题主要考查等腰三角形的性质及勾股定理的运用.注意正确地进行分类,考虑到所有的可能情况是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
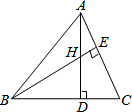 如图,已知AD和BE都是△ABC的高,且AD=BD,AC=4,H是高AD和BE的交点,则线段BH的长度为( )
如图,已知AD和BE都是△ABC的高,且AD=BD,AC=4,H是高AD和BE的交点,则线段BH的长度为( )| A. | 3 | B. | 4 | C. | 3.5 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com