Question

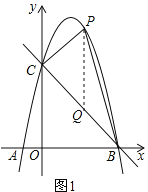
【题目】如图1，抛物线y=ax2+bx﹣4a经过A（﹣1，0）、C（0，4）两点，与x轴交于另一点B．

（1）求抛物线和直线BC的解析式；

（2）如图2，点P为第一象限抛物线上一点，是否存在使△PBC面积最大的点P？若存在，求出点P的坐标；若不存在，请说明理由；

（3）如图3，若抛物线的对称轴EF（E为抛物线顶点）与直线BC相交于点F，M为直线BC上的任意一点，过点M作MN∥EF交抛物线于点N，以E，F，M，N为顶点的四边形能否为平行四边形？若能，求点N的坐标；若不能，请说明理由．

Answer 1

【答案】（1）抛物线的解析式：y=﹣x2+3x+4．（2）存在，当P（2，6）时，△PCB的面积最大；（3）存在，点N坐标为（，）、（，），（，）．

【解析】

试题分析：（1）根据抛物线y=ax2+bx﹣4a经过A（﹣1，0）、C（0，4）两点，列出a和b的二元一次方程组，求出a和b的值，进而求出点B的坐标，即可求出直线BC的解析式；

（2）过点P作PQ∥y轴，交直线BC于Q，设P（x，﹣x2+3x+4），则Q（x，﹣x+4）；求出PQ的长，利用S△PCB=PQOB列出S关于x的二次函数，利用函数的性质求出面积的最大值，进而求出点P的坐标；

（3）首先求出EF的长，设N（x，﹣x2+3x+4），则M（x，﹣x+4），利用平行四边形对边平行且相等列出x的一元二次方程，解方程求出x的值即可．

解：（1）依题意，有：，

解得．

∴抛物线的解析式：y=﹣x2+3x+4．

∴由B（4，0）、C（0，4）可知，直线BC：y=﹣x+4；

（2）由B（4，0）、C（0，4）可知，直线BC：y=﹣x+4；

如图1，过点P作PQ∥y轴，交直线BC于Q，设P（x，﹣x2+3x+4），则Q（x，﹣x+4）；

∴PQ=（﹣x2+3x+4）﹣（﹣x+4）=﹣x2+4x；

S△PCB=PQOB=×（﹣x2+4x）×4=﹣2（x﹣2）2+8；

∴当P（2，6）时，△PCB的面积最大；

（3）存在．

抛物线y=﹣x2+3x+4的顶点坐标E（，），

直线BC：y=﹣x+4；当x=时，F（，），

∴EF=．

如图2，过点M作MN∥EF，交直线BC于M，设N（x，﹣x2+3x+4），则M（x，﹣x+4）；

∴MN=|（﹣x2+3x+4）﹣（﹣x+4）|=|﹣x2+4x|；

当EF与NM平行且相等时，四边形EFMN是平行四边形，

∴|﹣x2+4x|=；

由﹣x2+4x=时，解得x1=，x2=（不合题意，舍去）．

当x=时，y=﹣（）2+3×+4=，

∴N1（，）．

当﹣x2+4x=﹣时，解得x=，

当x=时，y=，

∴N2（，），

当x=时，y=，

即N3（，），

综上所述，点N坐标为（，）、（，），（，）．