Question

8．如图，已知AB为⊙O的直径，CD、CB为的切线，D、B为切点，连接AD、BD，OC交于点E，AE交BD于G，AE的延长线交BC于点F，给出下列结论：①AD∥OC；②点E为△CDB的内心；③EG=EF；④FC=FE，其中正确的是（　　）

• A． ①
• B． ①②
• C． ①②③
• D． ①②③④

Answer 1

分析 ①根据切线长定理，证△COB≌△COD，可得∠DCO=∠BCO．故OC⊥BD．根据圆周角定理即可得出AD⊥BD，由此可证得AD∥OC；
②连接DE、BE；上面已证得弧DE=弧BE，根据弦切角定理以及圆周角定理相等，易求得DE、BE分别平分∠CDB和∠CBD；根据三角形内心的定义，即可得出结论②正确；
③根据圆周角定理得到，GF⊥BE．又由②知，BE是∠CBD的平分线，根据等腰三角形的“三合一”性质得到EG=EF．故③正确；
④若FE=FC，则∠OCB=∠CEF=∠OEA=∠OAE，在Rt△OBC中，BD⊥OC，易得∠DBA=∠OCB（因为OC⊥BD），即∠DBA=∠EAB；因此弧BE=弧AD，而这个条件并不一定成立．故④不正确．

解答 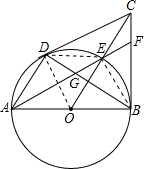解：①连接OD，DE，EB．CD与BC是⊙O的切线，易证△CDO≌△CBO，则∠DCO=∠BCO．故OC⊥BD．
∵AB是直径，
∴AD⊥BD，
∴AD∥OC，故①正确；

②∵CD是⊙O的切线，
∴∠CDE=$\frac{1}{2}$∠DOE，而∠BDE=$\frac{1}{2}$∠BOE，
∴∠CDE=∠BDE，即DE是∠CDB的角平分线，同理可证得BE是∠CBD的平分线，
因此E为△CBD的内心，故②正确；

③如图，∵AB是直径，
∴∠AEB=90°，即GF⊥BE．
又由②知，BE是∠CBD的平分线，
∴BE是等腰△GBF的边GF上的中垂线，则EG=EF．故③正确；

④若FC=FE，则应有∠OCB=∠CEF，应有∠CEF=∠AEO=∠EAB=∠DBA=∠DEA，
∴$\widehat{AD}$=$\widehat{BE}$，而$\widehat{AD}$与$\widehat{BE}$不一定相等，故④不正确．
故选C．

点评 本题考查了圆的综合题．解题时，利用了切线长定理，全等三角形的判定和性质，圆周角定理，弦切角定理，内心的概念求解．