
【题目】如图所示,已知∠1=115°,∠2=50°,∠3=65°,又∠NEG=∠GEB,试判断AB∥CD,EG∥FH是否成立,并说明理由.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某种子培育基地用A,B,C,D四种型号的小麦种子共2000粒进行发芽实验,从中选出发芽率高的种子进行推广.通过实验得知,C型号种子的发芽率为95%,根据实验数据绘制了图1和图2两幅尚不完整的统计图. 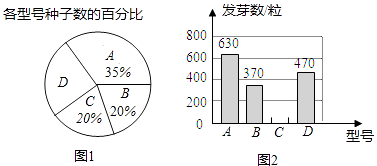
(1)D型号种子的粒数是粒;
(2)A型号种子的发芽率为;
(3)请你将图2的统计图补充完整;
(4)若将所有已发芽的种子放到一起,从中随机取出一粒,求取到B型号发芽种子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l分别交x轴、y轴于点A、B,交曲线y= ![]() (x>0)于点C,若AB:AC=1:3,且S△AOB=
(x>0)于点C,若AB:AC=1:3,且S△AOB= ![]() ,则k的值为( )
,则k的值为( )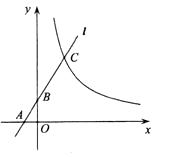
A.![]()
B.2 ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在楼房MN前有两棵树与楼房在同一直线上,且垂直于地面,为了测量树AB,CD的高度,小明爬到楼房顶部M处,光线恰好可以经过树CD的顶部C点到达树AB的底部B点,俯角为45°,此时小亮测得太阳光线恰好经过树CD的顶部C点到达楼房的底部N点,与地面的夹角为30°,树CD的影长DN为15米.请求出树AB、CD的高度?(结果保留根号)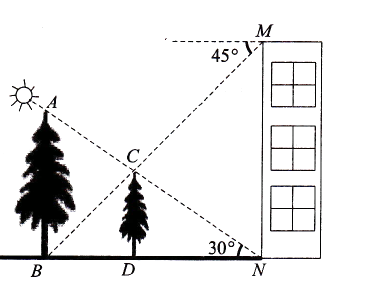
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技公司研发出一款多型号的智能手表,一家代理商出售该公司的A型智能手表去年销售总额为80000元,今年A型智能手表的售价每只比去年降低了600元,若售出的数量与去年相同,销售总额将比去年减少了25%.
(1)请问今年A型智能手表每只售价多少元?
(2)今年这家代理商准备新进一批A型智能手表和B型智能手表共100只,它们的进货价格与销售价格如表.若B型智能手表进货量不超过A型智能手表数量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
A型智能手表 | B型智能手表 | |
进价 | 1300元/只 | 1500元/只 |
售价 | 今年的售价 | 2300元/只 |
查看答案和解析>>
科目:初中数学 来源: 题型:
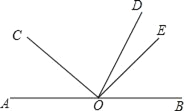
【题目】如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°.
(1)若∠AOC=48°,求∠DOE的度数.
(2)若∠AOC=α,则∠DOE= (用含α的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 ![]() ,在射线
,在射线 ![]() 上取点
上取点 ![]() ,以
,以 ![]() 为圆心的圆与
为圆心的圆与 ![]() 相切;在射线
相切;在射线 ![]() 上取点
上取点 ![]() ,以
,以 ![]() 为圆心,
为圆心, ![]() 为半径的圆与
为半径的圆与 ![]() 相切;在射线
相切;在射线 ![]() 上取点
上取点 ![]() ,以
,以 ![]() 为圆心,
为圆心, ![]() 为半径的圆与
为半径的圆与 ![]() 相切;
相切; ![]() ;在射线
;在射线 ![]() 上取点
上取点 ![]() ,以
,以 ![]() 为圆心,
为圆心, ![]() 为半径的圆与
为半径的圆与 ![]() 相切.若
相切.若 ![]() 的半径为
的半径为 ![]() ,则
,则 ![]() 的半径长是 .
的半径长是 . 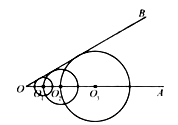
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空:

(1)∠1和∠3是直线________被直线____所截得的______;
(2)∠1和∠4是直线_________被直线____所截得的______;
(3)∠B和∠2是直线_________被直线_____所截得的______;
(4)∠B和∠4是直线_________被直线_____所截得的_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
根据以上信息,解答下列问题:
(1)设租车时间为 ![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为 ![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为 ![]() 元,分别求出
元,分别求出 ![]() ,
, ![]() 关于
关于 ![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com