
【题目】如图,已知 ![]() ,在射线
,在射线 ![]() 上取点
上取点 ![]() ,以
,以 ![]() 为圆心的圆与
为圆心的圆与 ![]() 相切;在射线
相切;在射线 ![]() 上取点
上取点 ![]() ,以
,以 ![]() 为圆心,
为圆心, ![]() 为半径的圆与
为半径的圆与 ![]() 相切;在射线
相切;在射线 ![]() 上取点
上取点 ![]() ,以
,以 ![]() 为圆心,
为圆心, ![]() 为半径的圆与
为半径的圆与 ![]() 相切;
相切; ![]() ;在射线
;在射线 ![]() 上取点
上取点 ![]() ,以
,以 ![]() 为圆心,
为圆心, ![]() 为半径的圆与
为半径的圆与 ![]() 相切.若
相切.若 ![]() 的半径为
的半径为 ![]() ,则
,则 ![]() 的半径长是 .
的半径长是 . 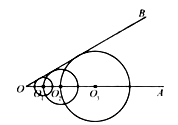
【答案】512
【解析】解:如图,连接O1A1,O2A2,O3A3,
∵⊙O1,⊙O2,⊙O3,……都与OB相切,
∴ O1A1⊥OB,
又∵∠AOB=30°,O1A1=r1=1=20.
∴OO1=2,
在Rt△OO2A2中,
∴OO1+O1O2=O2A2.
∴2+O2A2=2O2A2.
∴O2A2=r2=2=21.
∴OO2=4=22,
……
依此类推可得OnAn=rn=2=2n-1.
∴O10A10=r10=2=210-1=29=512.
所以答案是512.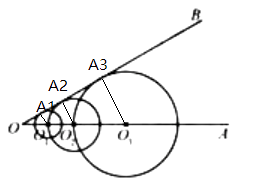
【考点精析】根据题目的已知条件,利用数与式的规律和含30度角的直角三角形的相关知识可以得到问题的答案,需要掌握先从图形上寻找规律,然后验证规律,应用规律,即数形结合寻找规律;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=m(x+1)(x﹣2)(m为常数,且m>0)与x轴从左至右依次交于A、B两点,与y轴交于点C,且OA=OC,经过点B的直线与抛物线的另一交点D在第二象限.
(1)求抛物线的函数表达式.
(2)若∠DBA=30°,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探索新知)
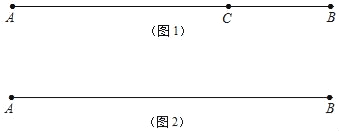
如图1,点C在线段AB上,图中共有3条线段:AB、AC和BC,若其中有一条线段的长度是另一条线段长度的两倍,则称点C是线段AB的“二倍点”.
(1)一条线段的中点 这条线段的“二倍点”;(填“是”或“不是”)
(深入研究)
如图2,若线段AB=20cm,点M从点B的位置开始,以每秒2cm的速度向点A运动,当点M到达点A时停止运动,运动的时间为t秒.
(2)问t为何值时,点M是线段AB的“二倍点”;
(3)同时点N从点A的位置开始,以每秒1cm的速度向点B运动,并与点M同时停止.请直接写出点M是线段AN的“二倍点”时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, AC BC , BD AD ,垂足分别为C 、D , AC BD , AC 、BD 交于O
(1)求证: CAB DBA ;
(2)求证: SADO SBCO .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,已知△ABC 中,其中 A(0,﹣2),B(2,﹣4),C(4,﹣1).
(1)画出与△ABC 关于 y 轴对称的图形△A1B1C1;
(2)写出△A1B1C1 各顶点坐标;
(3)求△ABC 的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为( ) 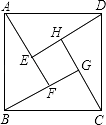
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com