练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    为支援灾区，某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件．已知B型学习用品的单价比A型学习用品的单价多10元，用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同．

    （1）求A、B两种学习用品的单价各是多少元？

    （2）若购买这批学习用品的费用不超过28000元，则最多购买B型学习用品多少件？


        解：（1）设A型学习用品单价x元，

    根据题意得：=，

    解得：x=20，

    经检验x=20是原方程的根，

    x+10=20+10=30．

    答：A型学习用品20元，B型学习用品30元；

    （2）设可以购买B型学习用品a件，则A型学习用品（1000﹣a）件，由题意，得：

    20（1000﹣a）+30a≤28000，

    解得：a≤800．

    答：最多购买B型学习用品800件．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    下列计算正确的是（　　）

    　   A．3x2•2x=6x3       B． x6÷x3=x2                C．                             （3a）2=3a2    D． （a+b）2=a2+b2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，将一条长度为1的线段三等分，然后取走其中的一份，称为第一次操作；再将余下的每一条线段三等分，然后取走其中一份，称为第二次操作；…如此重复操作，当第n次操作结束时，被取走的所有线段长度之和为　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，从一块直径是8m的圆形铁皮上剪出一个圆心角为90°的扇形，将剪下的扇形围成一个圆锥，圆锥的高是（　　）m．

    　  A．4         B． 5               C．             D． 2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


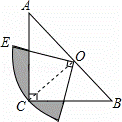
    如图，在△ABC中，∠C=90°，AC=BC，斜边AB=2，O是AB的中点，以O为圆心，线段OC的长为半径画圆心角为90°的扇形OEF，弧EH经过点C，则图中阴影部分的面积为　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


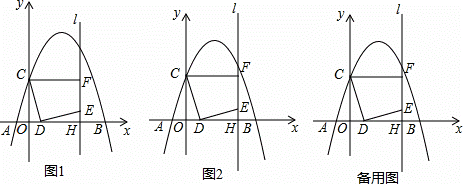
    如图1，在平面直角坐标系中，抛物线y=ax2+bx+3交x轴于A（﹣1，0）和B（5，0）两点，交y轴于点C，点D是线段OB上一动点，连接CD，将线段CD绕点D顺时针旋转90°得到线段DE，过点E作直线l⊥x轴于H，过点C作CF⊥l于F．

    （1）求抛物线解析式；

    （2）如图2，当点F恰好在抛物线上时，求线段OD的长；

    （3）在（2）的条件下：

    ①连接DF，求tan∠FDE的值；

    ②试探究在直线l上，是否存在点G，使∠EDG=45°？若存在，请直接写出点G的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，⊙O是△ABC的外接圆，⊙O的半径为3，∠A=45°，则的长是（　　）

    　   A．                          π B．                          π C．                          π      D． π

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    小明开了一家网店，进行社会实践，计划经销甲、乙两种商品．若甲商品每件利润10元，乙商品每件利润20元，则每周能卖出甲商品40件，乙商品20件．经调查，甲、乙两种商品零售单价分别每降价1元，这两种商品每周可各多销售10件．为了提高销售量，小明决定把甲、乙两种商品的零售单价都降价x元．

    （1）直接写出甲、乙两种商品每周的销售量y（件）与降价x（元）之间的函数关系式：y甲=　10x+40　，y乙=　10x+20　；

    （2）求出小明每周销售甲、乙两种商品获得的总利润W（元）与降价x（元）之间的函数关系式？如果每周甲商品的销售量不低于乙商品的销售量的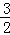，那么当x定为多少元时，才能使小明每周销售甲、乙两种商品获得的总利润最大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在四边形ABCD中，AB∥CD，连接BD，请添加一个适当的条件_____，使得

    ≌。（只需写一个）

    查看答案和解析>>

    同步练习册答案