
【题目】设a、b、c是直角三角形的三边,c为斜边,n为正整数,试判断an+bn与cn的关系,并证明你的结论.
【答案】解:当n=1,则a+b>c;
当n=2,则a2+b2=c2;
当n≥3,则an+bn<cn ,
证明如下:
∵sinA=![]() ,cosA=
,cosA=![]() ,
,
而0<sinA<1,0<cosA<1,
∴n≥3,sinnA<sin2A,connA<con2A,
∴sinnA+connA<sin2A+con2A=1,
即![]() +
+![]() <1,
<1,
∴an+bn<cn .
【解析】分类讨论:当n=1,根据三角形三边的关系有a+b>c;当n=2,根据勾股定理有n2+b2=c2;当n≥3,根据三角函数的定义得到
sinA=![]() , cosA=
, cosA=![]() , 且0<sinA<1,0<cosA<1,于是有sinnA<sin2A,connA<con2A,得到sinnA+connA<sin2A+con2A=1,
, 且0<sinA<1,0<cosA<1,于是有sinnA<sin2A,connA<con2A,得到sinnA+connA<sin2A+con2A=1,
即![]() +
+![]() <1,即可得到它们的关系.
<1,即可得到它们的关系.
【考点精析】本题主要考查了锐角三角函数的增减性的相关知识点,需要掌握当角度在0°~90°之间变化时:(1)正弦值随着角度的增大(或减小)而增大(或减小)(2)余弦值随着角度的增大(或减小)而减小(或增大)(3)正切值随着角度的增大(或减小)而增大(或减小)(4)余切值随着角度的增大(或减小)而减小(或增大)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】阅读下面一段文字:
问题:![]() 能化为分数形式吗?
能化为分数形式吗?
探求:步骤①设![]() ,步骤②
,步骤②![]() ,
,
步骤③![]() ,则
,则![]() ,
,
步骤④![]() ,解得:
,解得:![]() .
.
根据你对这段文字的理解,回答下列问题:
(1)步骤①到步骤②的依据是什么;
(2)仿照上述探求过程,请你尝试把![]() 化为分数形式:
化为分数形式:
(3)请你将![]() 化为分数形式,并说明理由.
化为分数形式,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求:A与A1,B与B1,C与C1相对应)
(2)在(1)问的结果下,连接BB1,CC1,求四边形BB1C1C的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的情况(记向东为正)记录如下(x>5且x<14,单位:m):
行驶次数 | 第一次 | 第二次 | 第三次 | 第四次 |
行驶情况 | x | ﹣ | x﹣3 | 2(5﹣x) |
行驶方向(填“东”或“西”) |
|
|
|
|
(1)请将表格补充完整;
(2)求经过连续4次行驶后,这辆出租车所在的位置;
(3)若出租车行驶的总路程为41m,求第一次行驶的路程x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将5张都是10元的纸币随机装入10个完全相同的信封中,设计以下几种抽奖游戏:
(1)游戏A:设计一个游戏,使任意抽取一个信封时,能抽到纸币的概率为![]() ;
;
(2)游戏B:设计一个游戏,使任意抽取一个信封时,能抽到纸币的概率为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的两边BC,AB分别在平面直角坐标系的x轴、y轴的正半轴上,正方形A′B′C′D′与正方形ABCD是以AC的中点O′为中心的位似图形,已知AC=3 ![]() ,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是( )
,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是( ) 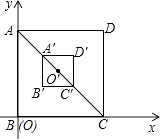
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com