Question

【题目】如图，已知△ABC是等腰三角形，其底边是BC，点D在线段AB上，E是CB延长线上一点，且∠DEC=∠DCE，F是AC上一点且DF∥BC，若∠A=60°．

求证：EB=AD．

Answer 1

【答案】证明见解析

【解析】

由平行线的性质得出∠ADF=∠ABC，∠AFD=∠ACB，∠FDC=∠DCE，证明△ABC是等边三角形，得出∠ABC=∠ACB=60°，证出△ADF是等边三角形，∠DFC=120°，得出AD=DF，由已知条件得出∠FDC=∠DEC，ED=CD，由AAS证明△DBE≌△CFD，得出EB=DF，即可得出结论．

∵DF∥BC，∴∠ADF=∠ABC，∠AFD=∠ACB，∠FDC=∠DCE．

∵△ABC是等腰三角形，∠A=60°，∴△ABC是等边三角形，∴∠ABC=∠ACB=60°，∴∠DBE=120°，∠ADF=∠AFD=60°=∠A，∴△ADF是等边三角形，∠DFC=120°，∴AD=DF．

∵∠DEC=∠DCE，∴∠FDC=∠DEC，ED=CD．

在△DBE和△CFD中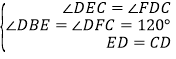，∵，∴△DBE≌△CFD（AAS），∴EB=DF，∴EB=AD．