
【题目】如图,在△ABC中,CE为三角形的角平分线,AD⊥CE于点F交BC于点D
(1) 若∠BAC=96°,∠B=28°,直接写出∠BAD=__________°
(2) 若∠ACB=2∠B
① 求证:AB=2CF
② 若EF=2,CF=5,直接写出![]() =__________
=__________

【答案】(1)34°;(2)①见解析,②![]()
【解析】
(1)在△ABC中,利用内角和可算出∠ACB,再由CE⊥AD,CE平分∠ACD,根据三线合一,可知△CAD为等腰三角形,即可求出底角∠CAD,进而求出∠BAD;
(2)①过A作AH∥BC,交CE的延长线于H,易得AH=AC,再由AD⊥CE,可得AD垂直平分CH,则CH=2CF,在由CH=CE+EH=BE+EH,而AE=EH,进而可得CH=BE+AE=AB,所以AB=2CF.
②易证△AHF≌△DCF,可得AH=CD,再由△AEH∽△BEH,得出相似比,进而得到![]() .
.
解:(1)在△ABC中,![]()
∵CE⊥AD,CE平分∠ACD
∴△CAD为等腰三角形,CA=CD
∴![]()
∴![]()
(2)①如图所示,过A作AH∥BC,交CE的延长线于H,
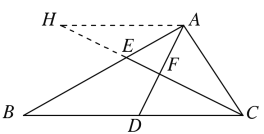
∵AH∥BC,∴∠H=∠BCE,∠B=∠BAH
又∵CH平分∠ACB,则∠ACH=∠BCH
∴∠H=∠ACH,∴AC=AH
又∵AF⊥CE,∴AD垂直平分CH,
∴CH=2CF
∵∠ACB=2∠B,∴∠B=∠BCE,∴BE=CE
又∵∠B=∠BAH,∴∠H=∠BAH,∴AE=HE
∴CH=CE+EH=BE+AE=AB
又∵CH=2CF
∴AB=2CF
②在△AHF和△DCF中,
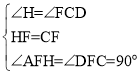
∴△AHF≌△DCF(ASA)
∴AH=CD
∵EF=2,CF=5,由①得BE=CE=CF+EF=7,AE=EH=HF-EF=5-2=3
又∵AH∥BC,∴![]() ,
,
∴![]() ,∴
,∴![]()


科目:初中数学 来源: 题型:
【题目】如图,在吴中区上方山动物园里有两只猴子在一棵树CD上的点B 处,且BC=5m,它们都要到池塘A处吃东西,其中一只猴子甲沿树爬至C再沿CA 走到离树24m处的池塘A处,另一只猴子乙先爬到树顶D处后再沿缆绳DA线段滑到A处.已知猴子甲所经过的路程比猴子乙所经过的路程多2m,设BD为xm.

(1)请用含有x的整式表示线段AD的长为 m;
(2)求这棵树高有多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等腰三角形,其底边是BC,点D在线段AB上,E是CB延长线上一点,且∠DEC=∠DCE,F是AC上一点且DF∥BC,若∠A=60°.
求证:EB=AD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量河对岸l1上两棵古树A、B之间的距离,某数学兴趣小组在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则A、B之间的距离为( )
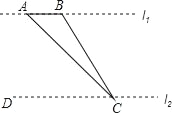
A. 50m B. 25m C. (50﹣![]() )m D. (50﹣25
)m D. (50﹣25![]() )m
)m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,画∠AOB=90°,并画∠AOB的平分线OC.

(1)将三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边与∠AOB的两边分别垂直,垂足为E、F(如图1).则PE_____PF(填“>”、“<”、“=”)
(2)把三角尺绕着点P旋转(如图2),PE与PF相等吗?试猜想PE、PF的大小关系,并说明理由.
(3)在(2)的条件下,过点P作直线GH⊥OC,分别交OA、OB于点G、H,如图3 .
①图中全等三角形有___________对(不添加辅助线)
②猜想GE2、FH2、EF2之间的关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两座城市相距100千米,现计划要在两座城市之间修筑一条高等级公路(即线段AB)。经测量,森林保护区中心P点在A城市的北偏东30°方向,B城市的北偏西45°方向上。已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内,请问:计划修筑的这条高等级公路会不会穿越保护区?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校未了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按![]() ,
,![]() ,
,![]() ,
,![]() 四个等级进行统计,制成了如下不完整的统计图.
四个等级进行统计,制成了如下不完整的统计图.

根据所给信息,解答以下问题
(1)在扇形统计图中,![]() 对应的扇形的圆心角是________度;
对应的扇形的圆心角是________度;
(2)补全条形统计图;
(3)该校九年级有300名学生,请估计足球运球测试成绩达到![]() 级的学生有多少人?
级的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com