
【题目】已知a、b、c满足:① ![]() 与2x2+ay3的和是单项式; ②
与2x2+ay3的和是单项式; ② ![]() ,
,
(1)求a、b、c的值;
(2)求代数式(5b2﹣3c2)﹣3(b2﹣c2)﹣(﹣c2)+2016abc的值.
【答案】
(1)解:∵﹣ ![]() x2yc+6与2x2+ay3的和是单项式,
x2yc+6与2x2+ay3的和是单项式, ![]() (b﹣5)2=0,
(b﹣5)2=0,
∴2+a=2,c+6=3,b﹣5=0,
解得:a=0,c=﹣3,b=5
(2)解:原式=5b2﹣3c2﹣3b2+3c2+c2+2016abc=2b2+c2+2016abc,
当a=0,c=﹣3,b=5时,原式=2×52+(﹣3)2+2016×0×5×(﹣3)=2×25+9+0=59
【解析】(1)根据两个单项式的和还是单项式可知这两个单项式是同类项,由同类项的定义可得关于a、c的方程,再根据平方的非负性可得关于b的方程,a、b、c的值可求;(2)根据去括号法则和合并同类项法则化简,再代值计算。
【考点精析】认真审题,首先需要了解去括号法则(去括号、添括号,关键要看连接号.扩号前面是正号,去添括号不变号.括号前面是负号,去添括号都变号),还要掌握代数式求值(求代数式的值,一般是先将代数式化简,然后再将字母的取值代入;求代数式的值,有时求不出其字母的值,需要利用技巧,“整体”代入)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
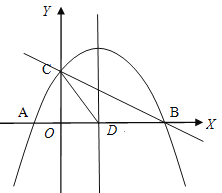
【题目】如图,抛物线![]() 与x轴交于A(-1,0)、B两点, 与y轴交于点C(0,2), 抛物线的对称轴交x轴于点D.
与x轴交于A(-1,0)、B两点, 与y轴交于点C(0,2), 抛物线的对称轴交x轴于点D.
(1)求抛物线的解析式;
(2)求sin∠ABC的值;
(3)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形,如果存在,直接写出点P的坐标;如果不存在,请说明理由;
(4)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时线段EF最长?求出此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H, 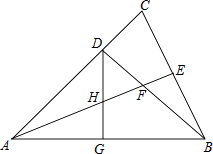
(1)求∠ACB的度数;
(2)HE= ![]() AF.
AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,天平呈平衡状态,其中左侧秤盘中有一袋玻璃球,右侧秤盘中也有一袋玻璃球,还有2个各20克的砝码.现将左侧袋中一颗玻璃球移至右侧秤盘,并拿走右侧秤盘的1个砝码后,天平仍呈平衡状态,如图2,则被移动的玻璃球的质量为( )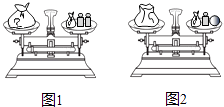
A.10克
B.15克
C.20克
D.25克
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=α(30°<α<45°),∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.
(1)如图,当α=40°,且射线OM在∠AOB的外部时,用直尺、量角器画出射线OD,ON的准确位置;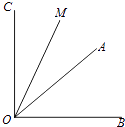
(2)求(1)中∠MON的度数,要求写出计算过程;
(3)当射线OM在∠AOB的内部时,用含α的代数式表示∠MON的度数.(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点B,C是x轴上的两个定点,∠ACB=90°,AC=BC,点A(l,3),点P是x轴上的一个动点,点E是AB的中点,在△PEF中,∠PEF=90°,PE=EF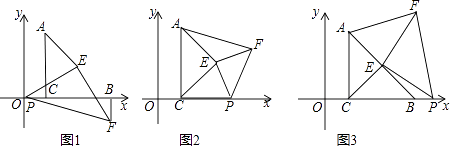
(1)如图1,当点P与坐标原点重合时:①求证△PCE≌△FBE;②求点F的坐标;
(2)如图2,当点P在线段CB上时,求证S△CPE=S△AEF
(3)如图3,当点P在线段CB的延长线时,若S△AEF=4S△PBE则此刻点F的坐标为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AB、CD交于点O,OE⊥AB于O,则下列不正确的是( ) 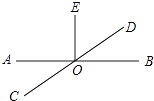
A.∠AOC与∠BOD是对顶角
B.∠BOD和∠DOE互为余角
C.∠AOC和∠DOE互为余角
D.∠AOE和∠BOC是对顶角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com