
【题目】甲、乙两个加工厂计划为某开发公司加工一批产品,已知甲、乙两个工厂每天分别能加工这种产品16件和24件,且单独加工这批产品甲厂比乙厂要多用20天,已知由甲厂单独做,公司需付甲厂每天费用180元;若由乙厂单独做,公司需付乙厂每天费用220元.
(1)求加工的这批产品共有多少件?
(2)若由一个加工厂单独加工完成,选用哪个加工厂费用较低?
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为12,E是BC中点,将正方形边CD沿DE折叠到DF,将AD折叠,使AD与DF重合,折痕交AB于G,连接BF,CF,则下列结论:①G、F、E三点共线;②BG=8;③△BEF∽△CDF;④S△BFG=![]() .其中正确的有( )
.其中正确的有( )
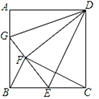
A. ①② B. ①②③ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,M,N分别为BC,CD的中点,AM=1,AN=2,∠MAN=60°,AM ,DC的延长线相交于点E,则AB的长为_____________;
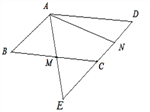
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平面直角坐标系中,![]() 、
、![]() ,现将线段
,现将线段![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得到点
得到点![]() ,连接
,连接![]() .
.
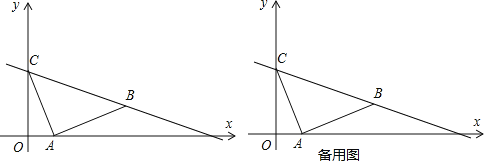
(1)求出直线![]() 的解析式;
的解析式;
(2)若动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以每分钟
以每分钟![]() 个单位的速度运动,过
个单位的速度运动,过![]() 作
作![]() 交
交![]() 轴于
轴于![]() ,连接
,连接![]() .设运动时间为
.设运动时间为![]() 分钟,当四边形
分钟,当四边形![]() 为平行四边形时,求
为平行四边形时,求![]() 的值.
的值.
(3)![]() 为直线
为直线![]() 上一点,在坐标平面内是否存在一点
上一点,在坐标平面内是否存在一点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为菱形,若存在,求出此时
为顶点的四边形为菱形,若存在,求出此时![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台.若商店保持两种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AC是对角线.将长方形ABCD绕点B顺时针旋转90°到长方形GBEF位置,H是EG的中点.若AB=6,BC=8,则线段CH的长为( )
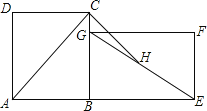
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在青山区“海绵城市”工程中,某工程队接受一段道路施工的任务,计划从2016年10月初至2017年9月底(12个月)完成.施工3个月后,实行倒计时,提高工作效率,剩余工程量与施工时间的关系如图所示,那么按提高工作效率后的速度做完全部工程,则工期可缩短________个月.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某地,人们发现某种蟋蟀1min,所叫次数x与当地温度T之间的关系或为T=ax+b,下面是蟋蟀所叫次数与温度变化情况对照表:
蟋蟀叫的次数(x) | … | 84 | 98 | 119 | … |
温度(℃)T | … | 15 | 17 | 20 | … |
①根据表中的数据确定a、b的值.
②如果蟋蟀1min叫63次,那么该地当时的温度约为多少摄氏度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某湖上风景区有两个观望点A,C和两个度假村B、D;度假村D在C正西方向,度假村B在C的南偏东![]() 方向,度假村B到两个观望点的距离都等于2km.
方向,度假村B到两个观望点的距离都等于2km.
(1)在图中标出A、B、C、D的位置,并写出道路CD与CB的夹角.
(2)如果度假村D到C是直公路,长为1km,D到A是环湖路,度假村B到两个观望点的总路程等于度假村D到两个观望点的总路程.求出环湖路的长.
(3)根据题目中的条件,能够判定![]() 吗?若能,请写出判断过程;若不能,请你添加一个条件,判定
吗?若能,请写出判断过程;若不能,请你添加一个条件,判定![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com