
【题目】如图,已知平面直角坐标系中,![]() 、
、![]() ,现将线段
,现将线段![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得到点
得到点![]() ,连接
,连接![]() .
.
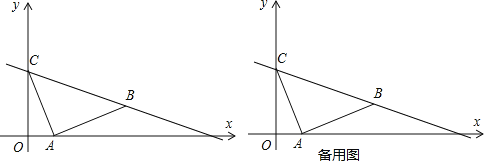
(1)求出直线![]() 的解析式;
的解析式;
(2)若动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以每分钟
以每分钟![]() 个单位的速度运动,过
个单位的速度运动,过![]() 作
作![]() 交
交![]() 轴于
轴于![]() ,连接
,连接![]() .设运动时间为
.设运动时间为![]() 分钟,当四边形
分钟,当四边形![]() 为平行四边形时,求
为平行四边形时,求![]() 的值.
的值.
(3)![]() 为直线
为直线![]() 上一点,在坐标平面内是否存在一点
上一点,在坐标平面内是否存在一点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为菱形,若存在,求出此时
为顶点的四边形为菱形,若存在,求出此时![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)t=
;(2)t=![]() s时,四边形ABMN是平行四边形;(3)存在,点Q坐标为:
s时,四边形ABMN是平行四边形;(3)存在,点Q坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)如图1中,作BH⊥x轴于H.证明△COA≌△AHB(AAS),可得BH=OA=1,AH=OC=2,求出点B坐标,再利用待定系数法即可解决问题.
(2)利用平行四边形的性质求出点N的坐标,再求出AN,BM,CM即可解决问题.
(3)如图3中,当OB为菱形的边时,可得菱形OBQP,菱形OBP1Q1.菱形OBP3Q3,当OB为菱形的对角线时,可得菱形OP2BQ2,点Q2在线段OB的垂直平分线上,分别求解即可解决问题.
(1)如图1中,作BH⊥x轴于H.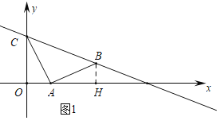
∵A(1,0)、C(0,2),
∴OA=1,OC=2,
∵∠COA=∠CAB=∠AHB=90°,
∴∠ACO+∠OAC=90°,∠CAO+∠BAH=90°,
∴∠ACO=∠BAH,
∵AC=AB,
∴△COA≌△AHB(AAS),
∴BH=OA=1,AH=OC=2,
∴OH=3,
∴B(3,1),
设直线BC的解析式为y=kx+b,则有![]() ,
,
解得: ,
,
∴![]() ;
;
(2)如图2中,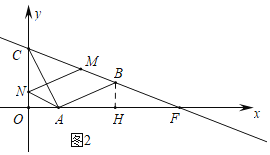
∵四边形ABMN是平行四边形,
∴AN∥BM,
∴直线AN的解析式为:![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵B(3,1),C(0,2),
∴BC=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴t=![]() s时,四边形ABMN是平行四边形;
s时,四边形ABMN是平行四边形;
(3)如图3中,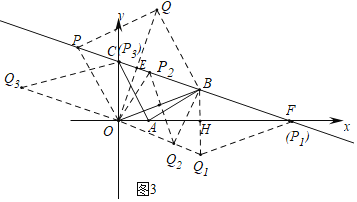
如图3中,当OB为菱形的边时,可得菱形OBQP,菱形OBP1Q1.菱形OBP3Q3,
连接OQ交BC于E,
∵OE⊥BC,
∴直线OE的解析式为y=3x,
由 ,解得:
,解得:![]() ,
,
∴E(![]() ,
,![]() ),
),
∵OE=OQ,
∴Q(![]() ,
,![]() ),
),
∵OQ1∥BC,
∴直线OQ1的解析式为y=-![]() x,
x,
∵OQ1=OB=![]() ,设Q1(m,-
,设Q1(m,-![]() ),
),
∴m2+![]() m2=10,
m2=10,
∴m=±3,
可得Q1(3,-1),Q3(-3,1),
当OB为菱形的对角线时,可得菱形OP2BQ2,点Q2在线段OB的垂直平分线上,
易知线段OB的垂直平分线的解析式为y=-3x+5,
由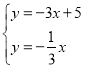 ,解得:
,解得: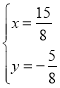 ,
,
∴Q2(![]() ,
,![]() ).
).
综上所述,满足条件的点Q坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】![]() 是线段
是线段![]() 上任一点,
上任一点,![]() ,
,![]() 两点分别从
两点分别从![]() 同时向
同时向![]() 点运动,且
点运动,且![]() 点的运动速度为
点的运动速度为![]() ,
,![]() 点的运动速度为
点的运动速度为![]() ,运动的时间为
,运动的时间为![]() .
.
(1)若![]() ,
,
①运动![]() 后,求
后,求![]() 的长;
的长;
②当![]() 在线段
在线段![]() 上运动时,试说明
上运动时,试说明![]() ;
;
(2)如果![]() 时,
时,![]() ,试探索
,试探索![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上有三个点![]() ,
,![]() ,
,![]() ,
,![]() 为原点,点
为原点,点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() .且
.且![]() 、
、![]() 满足
满足![]() .
.
(1)填空:![]() ;
;![]() .
.
(2)点![]() 把线段
把线段![]() 分成两条线段,其中一条是另一条线段的3倍,则
分成两条线段,其中一条是另一条线段的3倍,则![]() 的值为: .
的值为: .
(3)着![]() 为2,动点
为2,动点![]() 从点
从点![]() 出发,以每秒2个单位长度速度沿数轴负方向运动,同时,动点
出发,以每秒2个单位长度速度沿数轴负方向运动,同时,动点![]() 从点
从点![]() 出发,以每秒3个单位长度速度沿数轴正方向运动,求运动多少秒时点
出发,以每秒3个单位长度速度沿数轴正方向运动,求运动多少秒时点![]() 把线段
把线段![]() 分成两条线段且其中一条是另一条线段的3倍?
分成两条线段且其中一条是另一条线段的3倍?
查看答案和解析>>
科目:初中数学 来源: 题型:
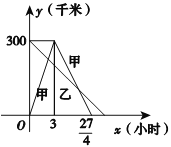
【题目】已知:甲乙两车分别从相距300千米的A,B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
(1)求甲车离出发地的距离y甲(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(2)若已知乙车行驶的速度是40千米/小时,它们在行驶过程中何时相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一副三角板,如图放置在桌面上,让三角板OAB的30°角顶点与三角板OCD的直角顶点重合,边OA与OC重合,固定三角板OCD不动,把三角板OAB绕着顶点O顺时针转动,直到边OB落在桌面上为止.

(1)如下图,当三角板OAB转动了20°时,求∠BOD的度数;
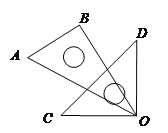
(2)在转动过程中,若∠BOD=20°,在下面两图中分别画出∠AOB的位置,并求出转动了多少度?
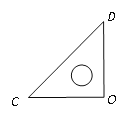

(3)在转动过程中,∠AOC与∠BOD有怎样的等量关系,请你给出相等关系式,并说明理由;


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,部分同学随家长一同到某公园游玩,下面是购买门票时,甲同学与其爸爸的对话(如图),试根据图中的信息,解决下列问题:
(1)本次共去了几个成人,几个学生?
(2)甲同学所说的另一种购票方式,是否可以省钱?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个加工厂计划为某开发公司加工一批产品,已知甲、乙两个工厂每天分别能加工这种产品16件和24件,且单独加工这批产品甲厂比乙厂要多用20天,已知由甲厂单独做,公司需付甲厂每天费用180元;若由乙厂单独做,公司需付乙厂每天费用220元.
(1)求加工的这批产品共有多少件?
(2)若由一个加工厂单独加工完成,选用哪个加工厂费用较低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如表所示.
所挂物体的质量 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
弹簧的长度 | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 |
(1)上表反映了哪些变量之间的关系?哪个是自变量,哪个是因变量?
(2)当物体的质量为2kg时,弹簧的长度是多少?
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(5)当物体的质量为2.5kg时,根据(4)的关系式,求弹簧的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若![]() ,且
,且![]() ,则我们称
,则我们称![]() 是
是![]() 的差余角.例如:若
的差余角.例如:若![]() ,则
,则![]() 的差余角
的差余角![]() .
.
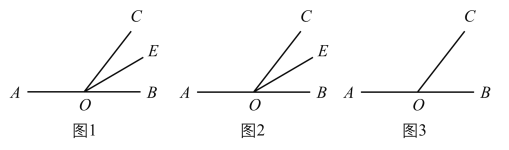
(1)如图1,点![]() 在直线
在直线![]() 上,射线
上,射线![]() 是
是![]() 的角平分线,若
的角平分线,若![]() 是
是![]() 的差余角,求
的差余角,求![]() 的度数.
的度数.
(2)如图2,点![]() 在直线
在直线![]() 上,若
上,若![]() 是
是![]() 的差余角,那么
的差余角,那么![]() 与
与![]() 有什么数量关系.
有什么数量关系.
(3)如图3,点![]() 在直线
在直线![]() 上,若
上,若![]() 是
是![]() 的差余角,且
的差余角,且![]() 与
与![]() 在直线
在直线![]() 的同侧,请你探究
的同侧,请你探究![]() 是否为定值?若是,请求出定值;若不是,请说明理由.
是否为定值?若是,请求出定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com