
【题目】定义:若![]() ,且
,且![]() ,则我们称
,则我们称![]() 是
是![]() 的差余角.例如:若
的差余角.例如:若![]() ,则
,则![]() 的差余角
的差余角![]() .
.
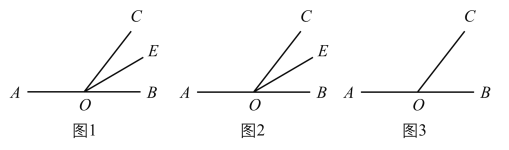
(1)如图1,点![]() 在直线
在直线![]() 上,射线
上,射线![]() 是
是![]() 的角平分线,若
的角平分线,若![]() 是
是![]() 的差余角,求
的差余角,求![]() 的度数.
的度数.
(2)如图2,点![]() 在直线
在直线![]() 上,若
上,若![]() 是
是![]() 的差余角,那么
的差余角,那么![]() 与
与![]() 有什么数量关系.
有什么数量关系.
(3)如图3,点![]() 在直线
在直线![]() 上,若
上,若![]() 是
是![]() 的差余角,且
的差余角,且![]() 与
与![]() 在直线
在直线![]() 的同侧,请你探究
的同侧,请你探究![]() 是否为定值?若是,请求出定值;若不是,请说明理由.
是否为定值?若是,请求出定值;若不是,请说明理由.
【答案】(1)30°;(2)![]() +
+![]() =90°;(3)为定值2,理由见解析
=90°;(3)为定值2,理由见解析
【解析】
(1)根据差余角的定义,结合角平分线的性质可得![]() 的度数;
的度数;
(2)根据差余角的定义得到![]() 和
和![]() 的关系,
的关系,
(3)分当OE在OC左侧时,当OE在OC右侧时,根据差余角的定义得到![]() 和
和![]() 的关系,再结合余角和补角的概念求出
的关系,再结合余角和补角的概念求出![]() 的值.
的值.
解:(1)如图,∵![]() 是
是![]() 的差余角
的差余角
∴![]() -
-![]() =90°,
=90°,
即![]() =
=![]() +90°,
+90°,
又∵![]() 是
是![]() 的角平分线,
的角平分线,
∴∠BOE=![]() ,
,
则![]() +90°+
+90°+![]() +
+![]() =180°,
=180°,
解得![]() =30°;
=30°;
(2)∵![]() 是
是![]() 的差余角,
的差余角,
∴![]() -
-![]() =90°,
=90°,
∵![]() =
=![]() +
+![]() ,
,![]() =
=![]() +
+![]() ,
,
∴![]() -
-![]() =90°,
=90°,
∵![]() =180°-
=180°-![]() ,
,
∴180°-![]() -
-![]() =90°,
=90°,
∴![]() +
+![]() =90°;
=90°;
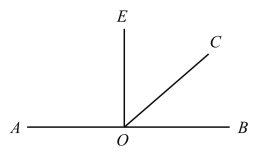
(3)当OE在OC左侧时,
∵![]() 是
是![]() 的差余角,
的差余角,
∴![]() -
-![]() =90°,
=90°,
∴∠AOE=∠BOE=90°,
则![]()
=![]()
=![]()
=2;
当OE在OC右侧时,
过点O作OF⊥AB,
∵![]() 是
是![]() 的差余角,
的差余角,
∴![]() =90°+
=90°+![]() ,
,
又∵![]() =90°+
=90°+![]() ,
,
∴![]() =
=![]() ,
,
∴![]()
=![]()
=![]()
=![]()
=![]()
=2.
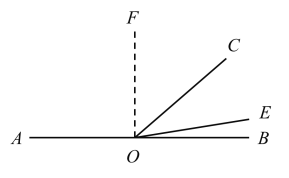
综上:![]() 为定值2.
为定值2.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】如图,已知平面直角坐标系中,![]() 、
、![]() ,现将线段
,现将线段![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得到点
得到点![]() ,连接
,连接![]() .
.
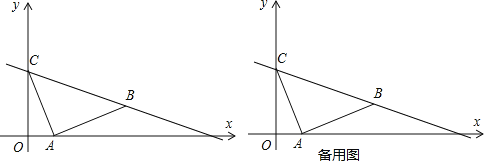
(1)求出直线![]() 的解析式;
的解析式;
(2)若动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以每分钟
以每分钟![]() 个单位的速度运动,过
个单位的速度运动,过![]() 作
作![]() 交
交![]() 轴于
轴于![]() ,连接
,连接![]() .设运动时间为
.设运动时间为![]() 分钟,当四边形
分钟,当四边形![]() 为平行四边形时,求
为平行四边形时,求![]() 的值.
的值.
(3)![]() 为直线
为直线![]() 上一点,在坐标平面内是否存在一点
上一点,在坐标平面内是否存在一点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为菱形,若存在,求出此时
为顶点的四边形为菱形,若存在,求出此时![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某地,人们发现某种蟋蟀1min,所叫次数x与当地温度T之间的关系或为T=ax+b,下面是蟋蟀所叫次数与温度变化情况对照表:
蟋蟀叫的次数(x) | … | 84 | 98 | 119 | … |
温度(℃)T | … | 15 | 17 | 20 | … |
①根据表中的数据确定a、b的值.
②如果蟋蟀1min叫63次,那么该地当时的温度约为多少摄氏度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,用3根火柴可拼成1个三角形,5根火柴可拼成2个三角形,7根火柴可拼成3个三角形……,按这个规律拼,用99根火柴可拼成____个三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
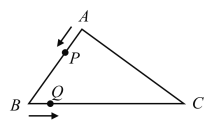
【题目】如图,在三角形![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发以2个单位长度/秒的速度沿
出发以2个单位长度/秒的速度沿![]() 的方向运动,点
的方向运动,点![]() 从点
从点![]() 沿
沿![]() 的方向与点
的方向与点![]() 同时出发;当点
同时出发;当点![]() 第一次回到
第一次回到![]() 点时,点
点时,点![]() ,
,![]() 同时停止运动;用
同时停止运动;用![]() (秒)表示运动时间.
(秒)表示运动时间.
(1)当![]() 为多少时,
为多少时,![]() 是
是![]() 的中点;
的中点;
(2)若点![]() 的运动速度是
的运动速度是![]() 个单位长度/秒,是否存在
个单位长度/秒,是否存在![]() 的值,使得
的值,使得![]() ;
;
(3)若点![]() 的运动速度是
的运动速度是![]() 个单位长度/秒,当点
个单位长度/秒,当点![]() ,
,![]() 是
是![]() 边上的三等分点时,求
边上的三等分点时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
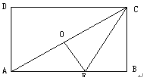
【题目】如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
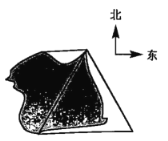
【题目】如图所示,某湖上风景区有两个观望点A,C和两个度假村B、D;度假村D在C正西方向,度假村B在C的南偏东![]() 方向,度假村B到两个观望点的距离都等于2km.
方向,度假村B到两个观望点的距离都等于2km.
(1)在图中标出A、B、C、D的位置,并写出道路CD与CB的夹角.
(2)如果度假村D到C是直公路,长为1km,D到A是环湖路,度假村B到两个观望点的总路程等于度假村D到两个观望点的总路程.求出环湖路的长.
(3)根据题目中的条件,能够判定![]() 吗?若能,请写出判断过程;若不能,请你添加一个条件,判定
吗?若能,请写出判断过程;若不能,请你添加一个条件,判定![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
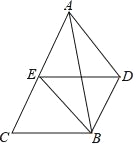
【题目】如图,已知DB∥AC,E是AC的中点,DB=AE,连结AD、BE.
(1)求证:四边形DBCE是平行四边形;
(2)若要使四边形ADBE是矩形,则△ABC应满足什么条件?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为![]() 的正方形的边长增加
的正方形的边长增加![]() ,得到一个边长为
,得到一个边长为![]() 的正方形.在图1的基础上,某同学设计了一个解释验证
的正方形.在图1的基础上,某同学设计了一个解释验证![]() 的方案(详见方案1)
的方案(详见方案1)
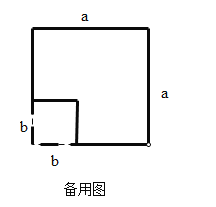
方案1.如图2,用两种不同的方式表示边长为![]() 的正方形的面积.
的正方形的面积.
方式1:![]()
方式2:![]()
因此,![]()
(1)请模仿方案1,在图1的基础上再设计一种方案,用以解释验证![]() ;
;
(2)如图3,在边长为![]() 的正方形纸片上剪掉边长为
的正方形纸片上剪掉边长为![]() 的正方形,请在此基础上再设计一个方案用以解释验证
的正方形,请在此基础上再设计一个方案用以解释验证![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com