
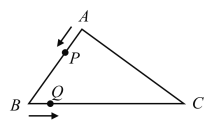
【题目】如图,在三角形![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发以2个单位长度/秒的速度沿
出发以2个单位长度/秒的速度沿![]() 的方向运动,点
的方向运动,点![]() 从点
从点![]() 沿
沿![]() 的方向与点
的方向与点![]() 同时出发;当点
同时出发;当点![]() 第一次回到
第一次回到![]() 点时,点
点时,点![]() ,
,![]() 同时停止运动;用
同时停止运动;用![]() (秒)表示运动时间.
(秒)表示运动时间.
(1)当![]() 为多少时,
为多少时,![]() 是
是![]() 的中点;
的中点;
(2)若点![]() 的运动速度是
的运动速度是![]() 个单位长度/秒,是否存在
个单位长度/秒,是否存在![]() 的值,使得
的值,使得![]() ;
;
(3)若点![]() 的运动速度是
的运动速度是![]() 个单位长度/秒,当点
个单位长度/秒,当点![]() ,
,![]() 是
是![]() 边上的三等分点时,求
边上的三等分点时,求![]() 的值.
的值.
【答案】(1)2;(2)存在,t=![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据AB的长度和点P的运动速度可以求得;
(2)根据题意可得:当![]() 时,点P在AB上,点Q在BC上,据此列出方程求解即可;
时,点P在AB上,点Q在BC上,据此列出方程求解即可;
(3)分两种情况:P为接近点A的三等分点,P为接近点C的三等分点,分别根据点的位置列出方程解得即可.
解:(1)∵![]() ,点P的运动速度为2个单位长度/秒,
,点P的运动速度为2个单位长度/秒,
∴当P为AB中点时,
![]() (秒);
(秒);
(2)由题意可得:当![]() 时,
时,
P,Q分别在AB,BC上,
∵点Q的运动速度为![]() 个单位长度/秒,
个单位长度/秒,
∴点Q只能在BC上运动,
∴BP=8-2t,BQ=![]() t,
t,
则8-2t=2×![]() t,
t,
解得t=![]() ,
,
当点P运动到BC和AC上时,不存在![]() ;
;
(3)当点P为靠近点A的三等分点时,如图,
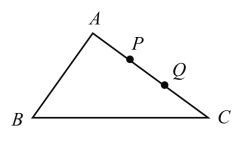
AB+BC+CP=8+16+8=32,
此时t=32÷2=16,
∵BC+CQ=16+4=20,
∴a=20÷16=![]() ,
,
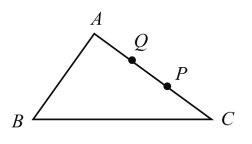
当点P为靠近点C的三等分点时,如图,
AB+BC+CP=8+16+4=28,
此时t=28÷2=14,
∵BC+CQ=16+8=24,
∴a=24÷14=![]() .
.
综上:a的值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
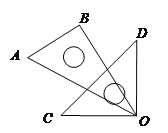
【题目】如图,将一副三角板,如图放置在桌面上,让三角板OAB的30°角顶点与三角板OCD的直角顶点重合,边OA与OC重合,固定三角板OCD不动,把三角板OAB绕着顶点O顺时针转动,直到边OB落在桌面上为止.

(1)如下图,当三角板OAB转动了20°时,求∠BOD的度数;
(2)在转动过程中,若∠BOD=20°,在下面两图中分别画出∠AOB的位置,并求出转动了多少度?
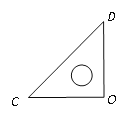

(3)在转动过程中,∠AOC与∠BOD有怎样的等量关系,请你给出相等关系式,并说明理由;


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件.已知生产一件A种产品需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件B种产品需用甲种原料4千克、乙种原料10千克,可获利润1200元。设生产A种产品的生产件数为x, A、B两种产品所获总利润为y (元)
(1)试写出y与x之间的函数关系式;
(2)求出自变量x的取值范围;
(3)利用函数的性质说明哪种生产方案获总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(-3,0)、B(1,0)、C(0,3)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足点为E,连接AE.
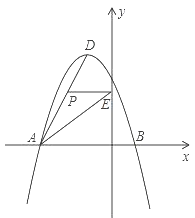
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取到最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P′,求出P′的坐标,并判断P′是否在该抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则以下四个结论中: ①△BDE是等边三角形; ②AE∥BC; ③△ADE的周长是9; ④∠ADE=∠BDC.其中正确的序号是( )
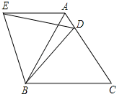
A.②③④B.①②④C.①②③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若![]() ,且
,且![]() ,则我们称
,则我们称![]() 是
是![]() 的差余角.例如:若
的差余角.例如:若![]() ,则
,则![]() 的差余角
的差余角![]() .
.
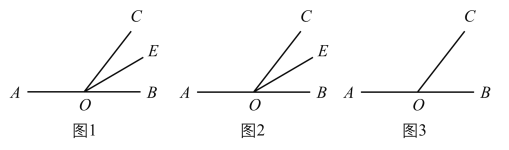
(1)如图1,点![]() 在直线
在直线![]() 上,射线
上,射线![]() 是
是![]() 的角平分线,若
的角平分线,若![]() 是
是![]() 的差余角,求
的差余角,求![]() 的度数.
的度数.
(2)如图2,点![]() 在直线
在直线![]() 上,若
上,若![]() 是
是![]() 的差余角,那么
的差余角,那么![]() 与
与![]() 有什么数量关系.
有什么数量关系.
(3)如图3,点![]() 在直线
在直线![]() 上,若
上,若![]() 是
是![]() 的差余角,且
的差余角,且![]() 与
与![]() 在直线
在直线![]() 的同侧,请你探究
的同侧,请你探究![]() 是否为定值?若是,请求出定值;若不是,请说明理由.
是否为定值?若是,请求出定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
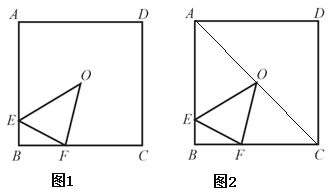
【题目】如图1,点O为正方形ABCD 的中心,E为AB 边上一点,F为BC边上一点,△EBF的周长等于 BC 的长.
(1)求∠EOF 的度数.
(2)连接 OA、OC(如图2).求证:△AOE∽△CFO.
(3)若OE=![]() OF,求
OF,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
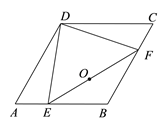
【题目】如图,菱形ABCD,∠A=60°,AB=6,点E,F分别是AB,BC边上沿某一方向运动的点,且DE=DF,当点E从A运动到B时,线段EF的中点O运动的路程为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
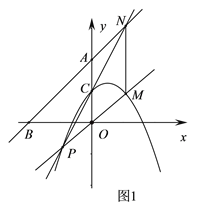
【题目】已知,抛物线y=-![]() x2 +bx+c交y轴于点C(0,2),经过点Q(2,2).直线y=x+4分别交x轴、y轴于点B、A.
x2 +bx+c交y轴于点C(0,2),经过点Q(2,2).直线y=x+4分别交x轴、y轴于点B、A.
(1)直接填写抛物线的解析式________;
(2)如图1,点P为抛物线上一动点(不与点C重合),PO交抛物线于M,PC交AB于N,连MN.
求证:MN∥y轴;
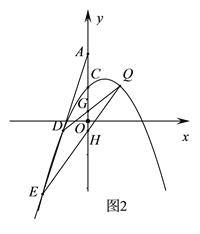
(3)如图,2,过点A的直线交抛物线于D、E,QD、QE分别交y轴于G、H.求证:CG CH为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com