练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，用3根火柴可拼成1个三角形，5根火柴可拼成2个三角形，7根火柴可拼成3个三角形……，按这个规律拼，用99根火柴可拼成____个三角形．

    【答案】49

    【解析】

    观察图形得到1个三角形所需火柴棍的根数=3，2个三角形所需火柴棍的根数=3+2，3个三角形所需火柴棍的根数=3+2×2，…，设99根火柴棍能拼成n个三角形，于是得到99=3+2×（n-1），解得n即可．

    解：∵1个三角形所需火柴棍的根数=3，
    2个三角形所需火柴棍的根数=3+2，
    3个三角形所需火柴棍的根数=3+2×2，
    …

    n个三角形所需火柴棍的根数=3+2×（n-1），
    设99根火柴棍能拼成n个三角形，
    ∴3+2×（n-1）=99．
    解得n=49．
    故答案为：49．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

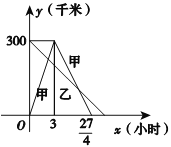
    【题目】已知：甲乙两车分别从相距300千米的A，B两地同时出发相向而行，其中甲到达B地后立即返回，如图是它们离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数图象．

    （1）求甲车离出发地的距离y甲（千米）与行驶时间x（小时）之间的函数关系式，并写出自变量的取值范围；

    （2）若已知乙车行驶的速度是40千米/小时，它们在行驶过程中何时相遇？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】弹簧挂上物体后会伸长，已知一弹簧的长度（cm）与所挂物体的质量（kg）之间的关系如表所示．

    所挂物体的质量

    0

    1

    2

    3

    4

    5

    6

    7

    弹簧的长度

    12

    12．5

    13

    13．5

    14

    14．5

    15

    15．5

    （1）上表反映了哪些变量之间的关系？哪个是自变量，哪个是因变量？

    （2）当物体的质量为2kg时，弹簧的长度是多少？

    （3）当物体的质量逐渐增加时，弹簧的长度怎样变化？

    （4）如果物体的质量为xkg，弹簧的长度为ycm，根据上表写出y与x的关系式；

    （5）当物体的质量为2．5kg时，根据（4）的关系式，求弹簧的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校与图书馆在冋一条笔直道路上，甲从学校去图书馆，乙从图书馆回学校，甲、乙两人都匀速步行且同时出发，乙先到达日的地．两人之间的距离y（米）与时间t（分钟）之间的函数关系如图所示．

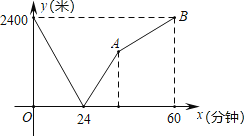
    （1）根据图象信息，当t＝　 　分钟时甲乙两人相遇，乙的速度为　 　米/分钟；

    （2）求点A的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在平面直角坐标系中，抛物线y=ax2+bx+c经过A（-3，0）、B（1，0）、C（0，3）三点，其顶点为D，连接AD，点P是线段AD上一个动点（不与A、D重合），过点P作y轴的垂线，垂足点为E，连接AE．

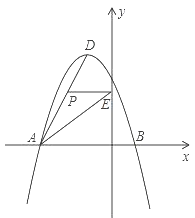
    （1）求抛物线的函数解析式，并写出顶点D的坐标；

    （2）如果P点的坐标为（x，y），△PAE的面积为S，求S与x之间的函数关系式，直接写出自变量x的取值范围，并求出S的最大值；

    （3）在（2）的条件下，当S取到最大值时，过点P作x轴的垂线，垂足为F，连接EF，把△PEF沿直线EF折叠，点P的对应点为点P′，求出P′的坐标，并判断P′是否在该抛物线上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了发展校园足球运动，某城区五校决定联合购买一批足球服和足球．经过市场调查发现：甲、乙两商场以同样的价格出售同种品牌的足球服和足球，已知每套足球服比每个足球多60元，两套足球服与三个足球的费用相等．经洽谈，甲商场的优惠方案是：每购买20套足球服，送一个足球；乙商场的优惠方案是：若购买足球服超过80套，则购买的足球打八折，若购买足球服不超过80套，不打折．

    （1）求每套足球服和每个足球的价格各是多少元；

    （2）若城区五校联合购买120套足球服和（）个足球，假如你是本次购买任务的负责人，你会选择到甲、乙两家中的哪一家商场购买更便宜？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：若，且，则我们称是的差余角．例如：若，则的差余角．

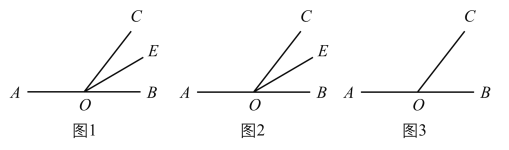
    （1）如图1，点在直线上，射线是的角平分线，若是的差余角，求的度数．

    （2）如图2，点在直线上，若是的差余角，那么与有什么数量关系．

    （3）如图3，点在直线上，若是的差余角，且与在直线的同侧，请你探究是否为定值？若是，请求出定值；若不是，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起（其中，，；）．

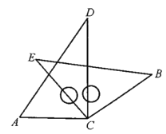
    （1）①若，则的度数为_____________；

    ②若，则的度数为_____________．

    （2）由（1）猜想与的数量关系，并说明理由．

    （3）当且点E在直线AC的上方时，这两块三角尺是否存在一组边互相平行？若存在，请写出角度所有可能的值（不必说明理由）；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学库存若干套桌椅，准备修理后支援贫困山区学校。现有甲、乙两木工组，甲每天修理桌椅16套，乙每天修桌椅比甲多8套，甲单独修完这些桌椅比乙单独修完多用20天，学校每天付甲组80元修理费，付乙组120元修理费。

    (1)该中学库存多少套桌椅？

    (2)在修理过程中，学校要派一名工人进行质量监督，学校负担他每天10元生活补助费，现有三种修理方案:a、由甲单独修理；b、由乙单独修理；c、甲、乙合作同时修理。你认为哪种方案省时又省钱？为什么？

    查看答案和解析>>

    同步练习册答案