
【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起(其中,![]() ,
,![]() ;
;![]() ).
).
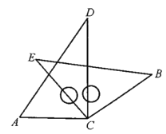
(1)①若![]() ,则
,则![]() 的度数为_____________;
的度数为_____________;
②若![]() ,则
,则![]() 的度数为_____________.
的度数为_____________.
(2)由(1)猜想![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(3)当![]() 且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出
且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出![]() 角度所有可能的值(不必说明理由);若不存在,请说明理由.
角度所有可能的值(不必说明理由);若不存在,请说明理由.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() ,理由详见解析;(3)∠ACE=45°或30°或120°或135°或165°
,理由详见解析;(3)∠ACE=45°或30°或120°或135°或165°
【解析】
(1)①先求出∠ACE,即可求出∠ACB;
②先求出∠ACE,即可求出∠DCE;
(2)根据题意可得![]() ,
,![]() ,从而求出
,从而求出![]() 与
与![]() 的数量关系;
的数量关系;
(3)根据平行线的判定定理和边的平行关系分类讨论,然后画出对应的图形即可得出结论.
解:(1)①∵![]() ,∠ACD=∠BCE=90°
,∠ACD=∠BCE=90°
∴∠ACE=∠ACD-∠DCE=45°
∴∠ACB=∠ACE+∠BCE=135°
故答案为:![]() .
.
②∵![]() ,∠ACD=∠BCE=90°
,∠ACD=∠BCE=90°
∴∠ACE=∠ACB-∠BCE=50°
∴∠DCE=∠ACD-∠ACE =40°
故答案为:![]() .
.
(2)![]() .理由如下
.理由如下
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]()
∴![]() .
.
(3)①当![]() 时,
时,
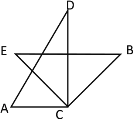
∵![]()
∴![]()
∴![]() ,
,
②当![]() 时,设CE与AD交于点F,如下图所示
时,设CE与AD交于点F,如下图所示

∵∠A=60°,∠BCE=90°
∴∠AFC=180°-∠ACE-∠A=90°
∴∠AFC=∠BCE
∴![]() .
.
③当![]() 时,如下图所示
时,如下图所示
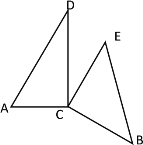
∵∠ACD=90°,∠D=30°
∴∠DCE=∠ACE-∠ACD=30°
∴∠DCE=∠D
∴![]() .
.
④当![]() 时,如下图所示
时,如下图所示

∵∠ACD=90°,∠E=45°
∴∠DCE=∠ACE-∠ACD=45°
∴∠DCE=∠E
∴![]() .
.
⑤当![]() 时,过点C作CG∥AD,如下图所示
时,过点C作CG∥AD,如下图所示

∴∠D=∠DCG=30°
∵∠ACD=90°,∠E=45°
∴∠GCE=∠ACE-∠ACD-∠DCG=45°
∴∠E=∠GCE
∴BE∥CG
∴![]() .
.
综上所述:∠ACE=45°或30°或120°或135°或165°.


科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AC是对角线.将长方形ABCD绕点B顺时针旋转90°到长方形GBEF位置,H是EG的中点.若AB=6,BC=8,则线段CH的长为( )
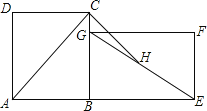
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,用3根火柴可拼成1个三角形,5根火柴可拼成2个三角形,7根火柴可拼成3个三角形……,按这个规律拼,用99根火柴可拼成____个三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
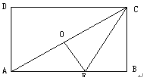
A. ![]() B.
B. ![]() C.
C. ![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
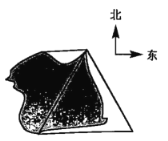
【题目】如图所示,某湖上风景区有两个观望点A,C和两个度假村B、D;度假村D在C正西方向,度假村B在C的南偏东![]() 方向,度假村B到两个观望点的距离都等于2km.
方向,度假村B到两个观望点的距离都等于2km.
(1)在图中标出A、B、C、D的位置,并写出道路CD与CB的夹角.
(2)如果度假村D到C是直公路,长为1km,D到A是环湖路,度假村B到两个观望点的总路程等于度假村D到两个观望点的总路程.求出环湖路的长.
(3)根据题目中的条件,能够判定![]() 吗?若能,请写出判断过程;若不能,请你添加一个条件,判定
吗?若能,请写出判断过程;若不能,请你添加一个条件,判定![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() )的图象交于点
)的图象交于点![]() .
.![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() . 一次函数的图象分别交
. 一次函数的图象分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、点
、点![]() ,且
,且![]() ,
,![]() .
.
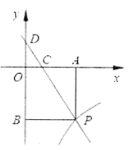
(1)求点![]() 的坐标;
的坐标;
(2)求一次函数与反比例函数的解析式;
(3)根据图象写出当![]() 取何值时,一次函数的值小于反比例函数的值?
取何值时,一次函数的值小于反比例函数的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
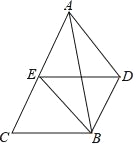
【题目】如图,已知DB∥AC,E是AC的中点,DB=AE,连结AD、BE.
(1)求证:四边形DBCE是平行四边形;
(2)若要使四边形ADBE是矩形,则△ABC应满足什么条件?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
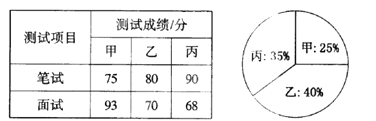
根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如上图所示,每得一票记作1分.
(l)请算出三人的民主评议得分;
(2)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确到 0.01 )?
(3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按 4 : 3 : 3 的比例确定个人成绩,那么谁将被录用?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com