
【题目】如图,四边形ABCD中,∠ABC=90°,AB=4,BC=3,CD=12,AD=13.求四边形ABCD的面积.

【答案】36
【解析】
连接AC,在直角三角形ABC中,由AB及BC的长,利用勾股定理求出AC的长,再由AD及CD的长,利用勾股定理的逆定理得到三角形ACD为直角三角形,根据四边形ABCD的面积=直角三角形ABC的面积+直角三角形ACD的面积,即可求出四边形的面积.
连接AC,如图所示:

∵∠B=90°,∴△ABC为直角三角形,
又AB=4,BC=3,
∴根据勾股定理得:AC=![]() =5,
=5,
又AD=13,CD=12,
∴AD2=132=169,CD2+AC2=122+52=144+25=169,
∴CD2+AC2=AD2,
∴△ACD为直角三角形,∠ACD=90°,
则S四边形ABCD=S△ABC+S△ACD=![]() ABBC+
ABBC+![]() ACCD=
ACCD=![]() ×3×4+
×3×4+![]() ×12×5=36.
×12×5=36.


科目:初中数学 来源: 题型:
【题目】学校与图书馆在冋一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达日的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.
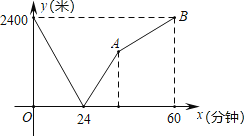
(1)根据图象信息,当t= 分钟时甲乙两人相遇,乙的速度为 米/分钟;
(2)求点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起(其中,![]() ,
,![]() ;
;![]() ).
).
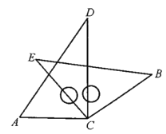
(1)①若![]() ,则
,则![]() 的度数为_____________;
的度数为_____________;
②若![]() ,则
,则![]() 的度数为_____________.
的度数为_____________.
(2)由(1)猜想![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(3)当![]() 且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出
且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出![]() 角度所有可能的值(不必说明理由);若不存在,请说明理由.
角度所有可能的值(不必说明理由);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
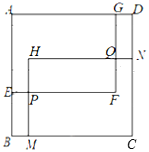
【题目】如图,在边长为6的正方形ABCD内部有两个大小相同的长方形AEFG、HMCN,HM与EF相交于点P,HN与GF相交于点Q,AG=CM=x,AE=CN=y.
(1)用含有x、y的代数式表示长方形AEFG与长方形HMCN重叠部分的面积S四边形HPFQ,并求出x应满足的条件;
(2)当AG=AE,EF=2PE时,
①AG的长为_______;
②四边形AEFG旋转后能与四边形HMCN重合,请指出该图形所在平面内能够作为旋转中心的所有点,并分别说明如何旋转的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:
垂直于同一直线的两条直线互相平行;![]() 的平方根是
的平方根是![]() ;若一个角的两边与另一个角的两边互相垂直,且其中一个角是45°,则另一个角为45°或135°;④若
;若一个角的两边与另一个角的两边互相垂直,且其中一个角是45°,则另一个角为45°或135°;④若![]() 是
是![]() 的整数部分,
的整数部分,![]() 是不等式
是不等式![]() 的最大整数解,则关于
的最大整数解,则关于![]() ,
,![]() 方程
方程![]() 的自然数解共有3对;⑤在平面直角坐标系中,点A、B的坐标分别为(2,0),(0,1),将线段AB平移至
的自然数解共有3对;⑤在平面直角坐标系中,点A、B的坐标分别为(2,0),(0,1),将线段AB平移至![]() ,
,![]() 的位置,则
的位置,则![]() .其中真命题的个数是( )
.其中真命题的个数是( )
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在直线AB上,OD是∠AOC的平分线,OE是∠BOC的平分线.
(1)图中与∠AOD互余的角是 ,与∠COE互补的角是 ;(把符合条件的角都写出来)
(2)求∠DOE的度数;
(3)如果∠BOF=51°34',∠COE=38°43',请画出射线OF,求∠COF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学库存若干套桌椅,准备修理后支援贫困山区学校。现有甲、乙两木工组,甲每天修理桌椅16套,乙每天修桌椅比甲多8套,甲单独修完这些桌椅比乙单独修完多用20天,学校每天付甲组80元修理费,付乙组120元修理费。
(1)该中学库存多少套桌椅?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:a、由甲单独修理;b、由乙单独修理;c、甲、乙合作同时修理。你认为哪种方案省时又省钱?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
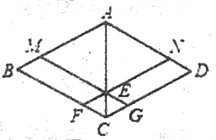
【题目】已知,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E;
(1)如图,求证:四边形AMEN是菱形;
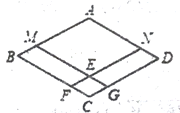
(2)如图,连接AC,在不添加任何辅助线的情况下,请直接写出面积相等的四边形;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】C点的坐标为(4,4),A为y轴负半轴上一动点,连CA,CB⊥CA交x轴于B.
(1)求OB﹣OA的值;
(2)E在x轴正半轴上,D在y轴负半轴上,∠DCE=45°,转动∠DCE,求线段BE、DE和AD之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com