
【题目】已知,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E;
(1)如图,求证:四边形AMEN是菱形;
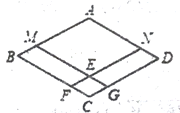
(2)如图,连接AC,在不添加任何辅助线的情况下,请直接写出面积相等的四边形;
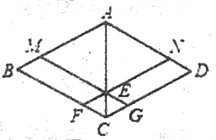
【答案】(1)见解析;(2)S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() .
.
【解析】
(1)由MG∥AD,NF∥AB,可证得四边形AMEN是平行四边形,又由四边形ABCD是菱形,BM=DN,可得AM=AN,即可证得四边形AMEN是菱形;
(2)易得四边形CGEF是菱形;即可得S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,继而求得答案.
,继而求得答案.
(1)证明:∵MG∥AD,NF∥AB,
∴四边形AMEN是平行四边形,
∴四边形ABCD是菱形,
∴AB=AD,
∵BM=DN,
∴ABBM=ADDN,
∴AM=AN,
∴四边形AMEN是菱形;
(2)∵四边形AMEN是菱形,
∴S![]() =S
=S![]() ,
,
同理:四边形CGEF是菱形,
∴S![]() =S
=S![]() ,
,
∵四边形ABCD是菱形,
∴S![]() =S
=S![]() ,
,
∴S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() .
.


 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
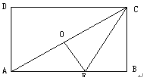
【题目】如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是△ABC的外心,I是△ABC的内心,连AI并延长交BC和⊙O于D、E两点.
(1)求证:EB=EI;
(2)若AB=4,AC=3,BE=2,求AI的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为![]() 的正方形的边长增加
的正方形的边长增加![]() ,得到一个边长为
,得到一个边长为![]() 的正方形.在图1的基础上,某同学设计了一个解释验证
的正方形.在图1的基础上,某同学设计了一个解释验证![]() 的方案(详见方案1)
的方案(详见方案1)
方案1.如图2,用两种不同的方式表示边长为![]() 的正方形的面积.
的正方形的面积.
方式1:![]()
方式2:![]()
因此,![]()
(1)请模仿方案1,在图1的基础上再设计一种方案,用以解释验证![]() ;
;
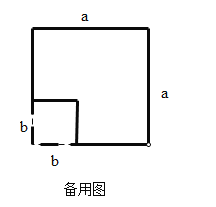
(2)如图3,在边长为![]() 的正方形纸片上剪掉边长为
的正方形纸片上剪掉边长为![]() 的正方形,请在此基础上再设计一个方案用以解释验证
的正方形,请在此基础上再设计一个方案用以解释验证![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的单位长度为1
![]()
(1)如果点![]() 表示的数互为相反数,那么点
表示的数互为相反数,那么点![]() 表示的数是_______,点
表示的数是_______,点![]() 表示的数是_______;
表示的数是_______;
(2)如果点![]() 表示的数互为相反数,那么四点中,点_______表示的数的绝对值最大,请简要说明理由;
表示的数互为相反数,那么四点中,点_______表示的数的绝对值最大,请简要说明理由;
(3)当点![]() 为原点时,若存在一点
为原点时,若存在一点![]() 到点
到点![]() 的距离是点
的距离是点![]() 到点
到点![]() 的距离的2倍,则点
的距离的2倍,则点![]() 所表示的数是_______.
所表示的数是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
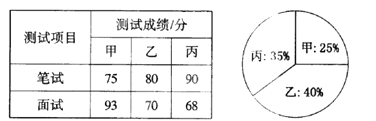
根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如上图所示,每得一票记作1分.
(l)请算出三人的民主评议得分;
(2)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确到 0.01 )?
(3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按 4 : 3 : 3 的比例确定个人成绩,那么谁将被录用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D是边BC上任意一点,连接AD,过点C作CE⊥AD于点E.
(1)如图1,若∠BAD=15°,且CE=1,求线段BD的长;
(2)如图2,过点C作CF⊥CE,且CF=CE,连接FE并延长交AB于点M,连接BF,求证:AM=BM.
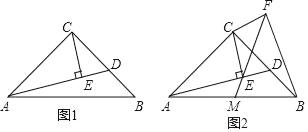
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com