
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

【答案】(1)抛物线的解析式为y=﹣2x2+x+3;(2)∠ACB=45°;(3)D(![]() ,
, ![]() ).
).
【解析】试题分析: (1)把点A、B、C的坐标分别代入已知抛物线的解析式列出关于系数的三元一次方程组
|
,通过解该方程组即可求得系数的值;
(2)由(1)中的抛物线解析式易求点M的坐标为(0,1).所以利用待定系数法即可求得直线AM的关系式为y=
1 |
3 |
x+1.由题意设点D的坐标为(x0,
1 |
3 |
x02
2 |
3 |
x0+1),则点F的坐标为(x0,
1 |
3 |
x0+1).易求DF=
1 |
3 |
x02
2 |
3 |
x0+1(
1 |
3 |
x0+1)=
1 |
3 |
x02x0=
1 |
3 |
(x0+
3 |
2 |
)2+
3 |
4 |
.根据二次函数最值的求法来求线段DF的最大值;
(3)需要对点P的位置进行分类讨论:点P分别位于第一、二、三、四象限四种情况.此题主要利用相似三角形的对应边成比例进行解答.
试题解析: 由题意可知
|
.解得
|
.
∴抛物线的表达式为y=-
1 |
3 |
x2
2 |
3 |
x+1.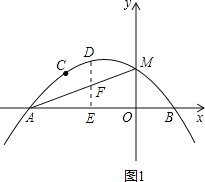
(2)将x=0代入抛物线表达式,得y=1.∴点M的坐标为(0,1).
设直线MA的表达式为y=kx+b,则
|
.
解得


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
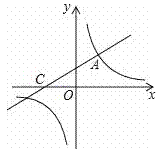
【题目】如图,直线![]() 与双曲线相交于点A(m,3),与x轴交于点C.
与双曲线相交于点A(m,3),与x轴交于点C.
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019 年 7 月 1 日,《上海市生活垃圾管理条例》正式实施,生活垃圾按照“可回收物”、 “有害垃圾”、“湿垃圾”、“干垃圾”的分类标准.没有垃圾分类和未指定投放到指定垃圾桶内等会被罚款和行政处罚.垃圾分类制度即将在全国范围内实施,很多商家推出售卖垃圾分类桶,某商店经销垃圾分类桶.现有如下信息:
信息 1:一个垃圾分类桶的售价比进价高 12 元;
信息 2:卖 3 个垃圾分类桶的费用可进货该垃圾分类桶 4 个;
请根据以上信息,解答下列问题:
(1)该商品的进价和售价各多少元?
(2)商店平均每天卖出垃圾分类桶 16 个.经调查发现,若销售单价每降低 1 元,每天可多售出 2 个.为了使每天获取更大的利润,垃圾分类桶的售价为多少元时,商店每天获取的利润最大?每天的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线ykx3经过点B(-![]() ,2),且与 x 轴交于点A.将抛物线
,2),且与 x 轴交于点A.将抛物线 ![]() 沿 x 轴作左右平移,记平移后的抛物线为C,其顶点为P.
沿 x 轴作左右平移,记平移后的抛物线为C,其顶点为P.
(1)求∠OAB 的度数;
(2)抛物线![]() 与直线 ykx3相交于 M,N两点,求△MON的面积.
与直线 ykx3相交于 M,N两点,求△MON的面积.
(3)在抛物线![]() 平移过程中,将△PAB 沿直线 AB 翻折得到△DAB,点D 能否落在抛物线C 上?如能,求出此时抛物线C 顶点P 的坐标;如不能,说明理由.
平移过程中,将△PAB 沿直线 AB 翻折得到△DAB,点D 能否落在抛物线C 上?如能,求出此时抛物线C 顶点P 的坐标;如不能,说明理由.
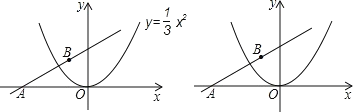
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先观察下列各式,再解答后面问题:
![]() =x2+11x+30;
=x2+11x+30;![]() =x2﹣11x+30;
=x2﹣11x+30;
![]() =x2+x﹣30;
=x2+x﹣30;![]() =x2﹣x﹣30;
=x2﹣x﹣30;
(1)根据以上各式呈现的规律,用公式表示出来,则![]() = ;
= ;
(2)试用你写的公式,直接写出下列两式的结果
①![]() = ;
= ;
②![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,直线EF分别与AB、CD交于点G,H,GM⊥EF,HN⊥EF,交AB于点N,∠1=50°.
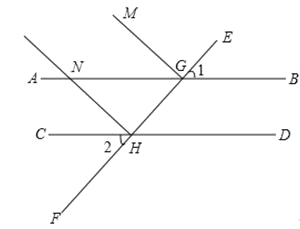
(1)求∠2的度数;
(2)试说明HN∥GM;
(3)∠HNG= .
查看答案和解析>>
科目:初中数学 来源: 题型:
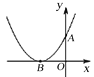
【题目】如图,已知二次函数![]() 的图象与y轴的正半轴交于点A,其顶点B在
的图象与y轴的正半轴交于点A,其顶点B在![]() 轴的负半轴上,且OA=OB,对于下列结论:①
轴的负半轴上,且OA=OB,对于下列结论:①![]() ≥0;②
≥0;②![]() ;③关于
;③关于![]() 的方程
的方程![]() 无实数根;④
无实数根;④![]() 的最小值为3.其中正确结论的个数为( )
的最小值为3.其中正确结论的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90°,且AD=12cm,AB=8cm,DC=10cm,若动点P从A点出发,以每秒2cm的速度沿线段AD向点D运动;动点Q从C点出发以每秒3cm的速度沿CB向B点运动,当P点到达D点时,动点P、Q同时停止运动,设点P、Q同时出发,并运动了t秒,回答下列问题:

(1)BC= cm;
(2)当t为多少时,四边形PQCD成为平行四边形?
(3)当t为多少时,四边形PQCD为等腰梯形?
(4)是否存在t,使得△DQC是等腰三角形?若存在,请求出t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上A,B两点对应的数分别为-2和8,P为数轴上一点,对应的数为x.
(1)线段PA的长度可表示为_________(用含![]() 的式子表示);
的式子表示);
(2)在数轴上是否存在点P,使得PA-PB=6?若存在,求出x的值;若不存在,请说明理由;
(3)当P为线段AB的中点时,点A,B,P同时开始在数轴上分别以每秒3个单位长度,每秒2个单位长度,每秒1个单位长度沿数轴正方向运动,试问经过几秒,PB=2PA?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com