
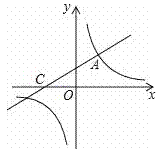
【题目】如图,直线![]() 与双曲线相交于点A(m,3),与x轴交于点C.
与双曲线相交于点A(m,3),与x轴交于点C.
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
【答案】(1)![]() ;(2)(﹣2,0)或(﹣6,0).
;(2)(﹣2,0)或(﹣6,0).
【解析】试题分析:(1)把A坐标代入直线解析式求出m的值,确定出A坐标,即可确定出双曲线解析式;
(2)设P(x,0),表示出PC的长,高为A纵坐标,根据三角形ACP面积求出x的值,确定出P坐标即可.
解:(1)把A(m,3)代入直线解析式得:3=![]() m+2,即m=2,
m+2,即m=2,
∴A(2,3),
把A坐标代入y=![]() ,得k=6,
,得k=6,
则双曲线解析式为y=![]() ;
;
(2)对于直线y=![]() x+2,令y=0,得到x=﹣4,即C(﹣4,0),
x+2,令y=0,得到x=﹣4,即C(﹣4,0),
设P(x,0),可得PC=|x+4|,
∵△ACP面积为3,
∴![]() |x+4|3=3,即|x+4|=2,
|x+4|3=3,即|x+4|=2,
解得:x=﹣2或x=﹣6,
则P坐标为(﹣2,0)或(﹣6,0).


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧)与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D,点E为y轴上一动点,CE的垂直平分线交抛物线于P,Q两点(点P在第三象限)

(1)求抛物线的函数表达式和直线BC的函数表达式;
(2)当△CDE是直角三角形,且∠CDE=90° 时,求出点P的坐标;
(3)当△PBC的面积为![]() 时,求点E的坐标.
时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
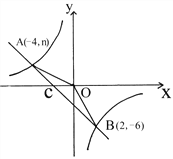
【题目】如图,已知A(-4,n)、B(2,-6)是一次函数y1=k1x+b与反比例函数y2=![]() 的两个交点,直线AB与x轴交于点C。
的两个交点,直线AB与x轴交于点C。
(1)求两函数解析式;(2)求△AOB的面积;
(3)根据图象回答:y1<y2时,自变量x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
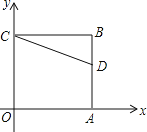
【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车收费标准:3 km以内(含3 km)起步价为8元,超过3 km后每1 km加收1.8元.
(1)若小明坐出租车行驶了6 km,则他应付多少元车费?
(2)如果用s表示出租车行驶的路程,m表示出租车应收的车费,请你表示出s与m之间的数量关系(s>3).
查看答案和解析>>
科目:初中数学 来源: 题型:
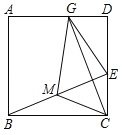
【题目】如图,在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有6张正面分别标有数字﹣1,0,1,2,3,4的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为a,则使得关于x的二次函数y=x2﹣2x+a﹣2与x轴有交点,且关于x的分式方程![]() 有解的概率为( )
有解的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)如图,点E、F为线段BD的两个三等分点,四边形AECF是菱形.

(1)试判断四边形ABCD的形状,并加以证明;
(2)若菱形AECF的周长为20,BD为24,试求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com