
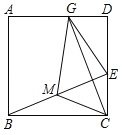
【题目】如图,在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为____.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】七年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项:评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:

(1)在这次评价中,一共抽查了________名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为________度;
(3)请将频数分布直方图补充完整;
(4)如果全市有8600名七年级学生,那么在试卷评讲课中,“独立思考”的七年级学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.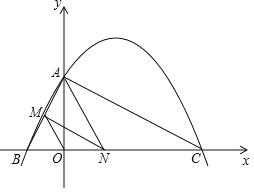
查看答案和解析>>
科目:初中数学 来源: 题型:
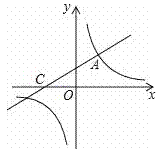
【题目】如图,直线![]() 与双曲线相交于点A(m,3),与x轴交于点C.
与双曲线相交于点A(m,3),与x轴交于点C.
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三(1)班要从2男2女共4名同学中选人做晨会的升旗手.
(1)若从这4人中随机选1人,则所选的同学性别为男生的概率是 .
(2)若从这4人中随机选2人,求这2名同学性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 ,∠E=∠F=90°,∠B=∠C,AC=AB,给出下列结论:① ∠1=∠2;② BE=CF;③ △ACN≌△ABM;④ CD=DN,其中正确的结论有( )个

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正常人的体温一般在37 ℃左右,但一天中的不同时刻不尽相同,如图所示反映了一天24小时内小红的体温变化情况,下列说法错误的是 ( )

A. 清晨5时体温最低
B. 下午5时体温最高
C. 这一天小红体温T(℃)的范围是36.5≤T≤37.5
D. 从5时至24时,小红体温一直是升高的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=3,CD=4,点P是AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥BC于点E,PF∥BC交AB于点F,连接EF,则EF的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,连接OD,∠AOD=∠APC.

(1)求证:AP是⊙O的切线;
(2)若⊙O的半径是4,AP=4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com