练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】正常人的体温一般在37 ℃左右,但一天中的不同时刻不尽相同,如图所示反映了一天24小时内小红的体温变化情况,下列说法错误的是 (　　)

    A. 清晨5时体温最低

    B. 下午5时体温最高

    C. 这一天小红体温T(℃)的范围是36.5≤T≤37.5

    D. 从5时至24时,小红体温一直是升高的

    【答案】D

    【解析】

    分析折线统计图，折线统计图中最底部的数据，则是温度最低的时刻，最高位置的数据则是温度最高的时刻；则清晨5时体温最低，下午5时体温最高；最高温度为37.5℃，最低温度为36.5℃，从5时到17时，小明的体温一直是升高的趋势，从而可求出答案．

    由图象可知图中最底部对应横轴上的数据则是体温最低的时刻，最高位置对应横轴上的数据则是体温最高的时刻，

    所以清晨5时体温最低，下午5时体温最高，故选项A、B正确，不符合题意；

    最高体温为37.5 ℃，最低体温为36.5 ℃，则小红这一天的体温范围是36.5≤T≤37.5，故C选项正确，不符合题意；

    从5时到17时，小红的体温一直是升高的趋势，而17时到24时的体温是下降的趋势，故D选项错误，符合题意，

    故选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】“安全教育平台”是中国教育学会为方便学长和学生参与安全知识活动、接受安全提醒的一种应用软件.某校为了了解家长和学生参与“防溺水教育”的情况，在本校学生中随机抽取部分学生作调查，把收集的数据分为以下4类情形：A.仅学生自己参与；B.家长和学生一起参与；

    C.仅家长自己参与； D.家长和学生都未参与.

    请根据图中提供的信息，解答下列问题：

    （1）在这次抽样调查中，共调查了________名学生；

    （2）补全条形统计图，并在扇形统计图中计算C类所对应扇形的圆心角的度数；

    （3）根据抽样调查结果，估计该校2000名学生中“家长和学生都未参与”的人数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市出租车收费标准：3 km以内(含3 km)起步价为8元，超过3 km后每1 km加收1.8元．

    (1)若小明坐出租车行驶了6 km，则他应付多少元车费？

    (2)如果用s表示出租车行驶的路程，m表示出租车应收的车费，请你表示出s与m之间的数量关系(s>3).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，E是边CD上一点(点E不与点C、D重合)，连结BE，取BE的中点M，连结CM．过点C作CG⊥BE交AD于点G，连结EG、MG．若CM=3，则四边形GMCE的面积为____．

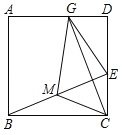
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个不透明的盒子里装有黑、白两种颜色的球共100只，这些球除颜色外其余完全相同．小颖做摸球实验，搅匀后，她从盒子里随机摸出一只球记下颜色后，再把球放回盒子中，不断重复上述过程，如表是实验中的一组统计数据：

    摸球的次数n

    100

    200

    300

    500

    800

    1000

    3000

    摸到白球的次数m

    70

    124

    190

    325

    538

    670

    2004

    摸到白球的频率

    0.70

    0.62

    0.633

    0.65

    0.6725

    0.670

    0.668

    （1）若从盒子里随机摸岀一只球，则摸到白球的概率的估计值为　　　　；(精确到0.01)

    （2）试估算盒子里黑球有　　　　只；

    （3）某小组在“用频率估计概率”的试验中，符合这一结果的试验最有可能的是　　　　．

    A．从一副扑克牌中任意抽取一张，这张牌是“红色的”

    B．掷一枚质地均匀的硬币，落地时结果是“正面朝上”

    C．掷一个质地均匀的正六面体骰子(面的点数标记分别为1到6)，落地时面朝上的点数小于5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现有6张正面分别标有数字﹣1，0，1，2，3，4的不透明卡片，它们除数字不同外其余全部相同．现将它们背面朝上，洗匀后从中任取一张，将该卡片上的数字记为a，则使得关于x的二次函数y=x2﹣2x+a﹣2与x轴有交点，且关于x的分式方程有解的概率为（　　）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

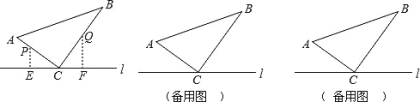
    【题目】如图，ABC 中，∠ACB=90°，AC=6cm，BC=8cm，点 P 从 A 点出发沿 A-C-B 路径向终点运动，终点为 B点；点 Q 从 B 点出发沿 B-C-A 路径向终点运动，终点为 A 点，点 P 和 Q 分别以 1cm/s 和 xcm / s 的运动速度 同时开始运动，两点都要到相应的终点时才能停止运动，在某时刻，分别过 P 和 Q 作 PE⊥ l 于 E，QF⊥ l 于 F.

    (1)如图，当 x 2 时，设点 P 运动时间为 ts ，当点 P 在 AC 上，点 Q 在 BC 上时：

    ①用含 t 的式子表示 CP 和 CQ，则 CP= cm，CQ= cm；

    ②当 t 2 时,PEC 与QFC 全等吗？并说明理由；

    (2)请问:当 x 3 时，PEC 与QFC 有没有可能全等？若能，直接写出符合条件的 t 的值；若不能，请说明 理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，D是△ABC的边AB上一点，CE∥AB，DE交AC于点F，若FA=FC．

    （1）求证：四边形ADCE是平行四边形；

    （2）若AE⊥EC，EF=EC=5，求四边形ADCE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了保护环境，某企业决定购买10台污水处理设备；现有A、B两种型号的设备，其中每台的价格、月处理污水量及年消耗费如下表：

    A型

    B型

    价格（万元/台）

    12

    10

    处理污水量（吨/月）

    240

    200

    年消耗费（万元/台）

    1

    1

    经预算，该企业购买设备的资金不高于105万元。

    （1） 请你设计该企业有几种购买方案；

    （2）若该企业每月产生的污水量为2040吨，为了节约资金，应选择哪种购买方案？

    查看答案和解析>>

    同步练习册答案