
【题目】如图,D是△ABC的边AB上一点,CE∥AB,DE交AC于点F,若FA=FC.
(1)求证:四边形ADCE是平行四边形;
(2)若AE⊥EC,EF=EC=5,求四边形ADCE的面积.

【答案】(1)见解析;(2)25![]()
【解析】
(1)首先利用ASA得出△DAF≌△ECF,进而利用全等三角形的性质得出CE=AD,即可得出四边形ACDE是平行四边形;(2)由AE⊥EC,四边形ADCE是平行四边形,可推出四边形ADCE是矩形,由F为AC的中点,求出AC,根据勾股定理即可求得AE,由矩形面积公式即可求得结论.
(1)证明:∵CE∥AB,
∴∠BAC=∠ECA,
在△DAF和△ECF中,
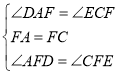
∴△DAF≌△ECF (ASA),
∴CE=AD,
∴四边形ADCE是平行四边形;
(2)∵AE⊥EC,四边形ADCE是平行四边形,
∴四边形ADCE是矩形,
在Rt△AEC中,F为AC的中点,
∴AC=2EF=10,
∴AE2=AC2-EC2=102-52=75,
∴AE=5![]() ,
,
∴四边形ADCE的面积=AEEC=25![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.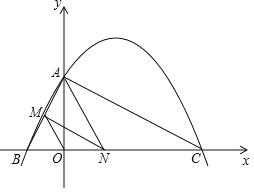
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正常人的体温一般在37 ℃左右,但一天中的不同时刻不尽相同,如图所示反映了一天24小时内小红的体温变化情况,下列说法错误的是 ( )

A. 清晨5时体温最低
B. 下午5时体温最高
C. 这一天小红体温T(℃)的范围是36.5≤T≤37.5
D. 从5时至24时,小红体温一直是升高的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=3,CD=4,点P是AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥BC于点E,PF∥BC交AB于点F,连接EF,则EF的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济南市地铁1号线于2019年1月1日起正式通车,在修建过程中,技术人员不断改进技术,提高工作效率,如在打通一条长600米的隧道时,计划用若干小时完成,在实际工作过程中,每小时打通隧道长度是原计划的1.2倍,结果提前2小时完成任务.
(1)求原计划每小时打通隧道多少米?
(2)如果按照这个速度下去,后面的300米需要多少小时打通?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中O是原点,平行四边形ABCO的顶点A、C的坐标分别(8,0)、(3,4),点D,E把线段OB三等分,延长CD、CE分别交OA、AB于点F,G,连接FG.则下列结论:①F是OA的中点;②△OFD与△BEG相似;③四边形DEGF的面积是![]() ;④
;④![]() .正确的个数是( )
.正确的个数是( )
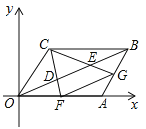
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,连接OD,∠AOD=∠APC.

(1)求证:AP是⊙O的切线;
(2)若⊙O的半径是4,AP=4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,将□ABCD放置在第一象限,且AB∥x轴,直线y=-x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图②所示,那么AD的长为__________.
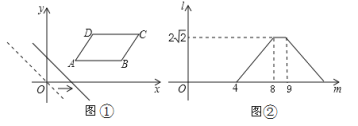
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com