
【题目】济南市地铁1号线于2019年1月1日起正式通车,在修建过程中,技术人员不断改进技术,提高工作效率,如在打通一条长600米的隧道时,计划用若干小时完成,在实际工作过程中,每小时打通隧道长度是原计划的1.2倍,结果提前2小时完成任务.
(1)求原计划每小时打通隧道多少米?
(2)如果按照这个速度下去,后面的300米需要多少小时打通?
【答案】(1)原计划每小时打通隧道50米.(2)按照这个速度下去,后面的300米需要5小时打通.
【解析】
(1)设原计划每小时打通隧道x米,则实际工作过程中每小时打通隧道1.2x米,根据工作时间=工作总量÷工作效率结合在打通一条长600米的隧道时实际比原计划提前2小时完成任务,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)根据工作时间=工作总量÷工作效率(提高工作效率后的工作效率),即可求出结论.
解:(1)设原计划每小时打通隧道x米,则实际工作过程中每小时打通隧道1.2x米,
依题意,得:![]() =2,
=2,
解得:x=50,
经检验,x=50是原方程的解,且符合题意.
答:原计划每小时打通隧道50米.
(2)300÷(50×1.2)=5(小时).
答:按照这个速度下去,后面的300米需要5小时打通.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有3个小球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个小球是白球的概率;
(2)摸出1个小球,记下颜色后放回,并搅均,再摸出1个小球.求两次摸出的小球恰好颜色不同的概率.(要求画树状图或列表)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有黑、白两种颜色的球共100只,这些球除颜色外其余完全相同.小颖做摸球实验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 70 | 124 | 190 | 325 | 538 | 670 | 2004 |
摸到白球的频率 | 0.70 | 0.62 | 0.633 | 0.65 | 0.6725 | 0.670 | 0.668 |
(1)若从盒子里随机摸岀一只球,则摸到白球的概率的估计值为 ;(精确到0.01)
(2)试估算盒子里黑球有 只;
(3)某小组在“用频率估计概率”的试验中,符合这一结果的试验最有可能的是 .
A.从一副扑克牌中任意抽取一张,这张牌是“红色的”
B.掷一枚质地均匀的硬币,落地时结果是“正面朝上”
C.掷一个质地均匀的正六面体骰子(面的点数标记分别为1到6),落地时面朝上的点数小于5.
查看答案和解析>>
科目:初中数学 来源: 题型:
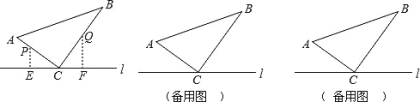
【题目】如图,![]() ABC 中,∠ACB=90°,AC=6cm,BC=8cm,点 P 从 A 点出发沿 A-C-B 路径向终点运动,终点为 B点;点 Q 从 B 点出发沿 B-C-A 路径向终点运动,终点为 A 点,点 P 和 Q 分别以 1cm/s 和 xcm / s 的运动速度 同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 P 和 Q 作 PE⊥ l 于 E,QF⊥ l 于 F.
ABC 中,∠ACB=90°,AC=6cm,BC=8cm,点 P 从 A 点出发沿 A-C-B 路径向终点运动,终点为 B点;点 Q 从 B 点出发沿 B-C-A 路径向终点运动,终点为 A 点,点 P 和 Q 分别以 1cm/s 和 xcm / s 的运动速度 同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 P 和 Q 作 PE⊥ l 于 E,QF⊥ l 于 F.
(1)如图,当 x 2 时,设点 P 运动时间为 ts ,当点 P 在 AC 上,点 Q 在 BC 上时:
①用含 t 的式子表示 CP 和 CQ,则 CP= cm,CQ= cm;
②当 t 2 时,![]() PEC 与
PEC 与![]() QFC 全等吗?并说明理由;
QFC 全等吗?并说明理由;
(2)请问:当 x 3 时,![]() PEC 与
PEC 与![]() QFC 有没有可能全等?若能,直接写出符合条件的 t 的值;若不能,请说明 理由。
QFC 有没有可能全等?若能,直接写出符合条件的 t 的值;若不能,请说明 理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元) | 180 | 260 | 280 | 300 |
y(间) | 100 | 60 | 50 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每间空置的客房,宾馆每日需支出各种费用60元.当房价为多少元时,宾馆当日利润最大?求出最大利润.(宾馆当日利润=当日房费收入-当日支出)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC的边AB上一点,CE∥AB,DE交AC于点F,若FA=FC.
(1)求证:四边形ADCE是平行四边形;
(2)若AE⊥EC,EF=EC=5,求四边形ADCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小莹、小亮准备参加中考模拟考试,学校规定考生每人占一个桌子,按考号人座.考号按如图方式贴在桌子上,请回答下面的问题:

(1)小莹的考号是13,小亮的考号是24,在图中对应的“□”中,请用他们的名字分别标出他们在考场内座位的位置;
(2)某同学座位的位置在第a行和第b列的相交的“□”处,用数对表示是(a,b),那么小莹的位置用数对表示是( ),小亮的位置用数对表示是( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F是四边形ABCD对角线AC上的两点,AD∥BC,DF∥BE,AE=CF.
求证:(1)△AFD≌△CEB;
(2)四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在菱形ABCD中,∠B=60°,M为AB的中点,动点P从点B出发,沿B→C→D的路径运动,到达点D时停止.连接MP,设点P运动的路程为x,MP2=y,若y与x的函数图象大致如图②所示,则菱形ABCD的周长为____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com