【题目】如图，E，F是四边形ABCD对角线AC上的两点，AD∥BC，DF∥BE，AE=CF．
求证：（1）△AFD≌△CEB；
（2）四边形ABCD是平行四边形．
科目：初中数学 来源： 题型：
【题目】小亮和小芳都想参加学校杜团组织的暑假实践活动，但只有一个名额，小亮提议用如下的办法决定谁去等加活动：将一个转盘9等分，分别标上1至9九个号码，随意转动转盘，
若转到2的倍数，小亮去参加活动；转到3的倍数，小芳去参加活动；转到其它号码则重新特动转盘．
（1）转盘转到2的倍数的概率是多少？
（2）你认为这个游戏公平吗？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，Rt△ABC≌Rt△EDF，∠ACB=∠F=90°，∠A=∠E=30°．△EDF绕着边AB的中点D旋转， DE，DF分别交线段AC于点M，K．
（1）观察： ①如图2、图3，当∠CDF=0° 或60°时，AM+CK_______MK(填“>”，“<”或“=”)．
②如图4，当∠CDF=30° 时，AM+CK___MK(只填“>”或“<”)．
（2）猜想：如图1，当0°＜∠CDF＜60°时，AM+CK_______MK，证明你所得到的结论．
（3）如果
，请直接写出∠CDF的度数和
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】商场某种商品平均每天可销售30件，每件盈利50元。为了尽快减少库存，商场决定采取适当的降价措施。经调查发现，每件商品每降价1元，商场平均每天可多售出2件。设每件商品降价
元。据此规律，请回答：
（1）商场日销售量增加_____件，每件商品盈利_____元（用含
的代数式表示）。
（2）在上述条件不变、销售正常情况下，每件商品降价多少元时，商场日盈利可达到2100元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，
，
，
为
边的中点，
，
绕点旋转，它的两边分别交
和
（或它们的延长线）于
，
.
（1）当
于时（如图1），可得
______________
.
（2）当
与不垂直时（如图2），第（1）小题得到的结论成立吗？若成立，请给予证明；若不成立，请直接给出
，
，的关系.
（3）当点在延长线上时（如图3），第（1）小题得到的结论成立吗？若成立，请给予证明；若不成立，请直接给出，，的关系.
查看答案和解析>>
科目：初中数学 来源： 题型：
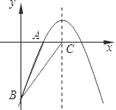
【题目】如图，已知二次函数y=﹣
+bx+c的图象经过A（2，0）、B（0，﹣6）两点．
（1）求这个二次函数的解析式；
（2）求当x满足什么条件时，函数值大于0？；
（3）设该二次函数的对称轴与x轴交于点C，连接BA、BC，求△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知A（﹣4，﹣1），B（﹣5，﹣4），C（﹣1，﹣3），△ABC经过平移得到的△A′B′C′，△ABC中任意一点P（x1，y1）平移后的对应点为P′（x1+6，y1+4）．
（1）请在图中作出△A′B′C′；
（2）写出点A′、B′、C′的坐标；
（3）求△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某基地计划新建一个矩形的生物园地，一边靠旧墙（墙足够长），另外三边用总长54米的不锈钢栅栏围成，与墙平行的一边留一个宽为2米的出入口，如图所示，如何设计才能使园地的而积最大？下面是两位学生争议的情境：请根据上面的信息，解决问题：
（1）设AB＝x米（x＞0），试用含x的代数式表示BC的长；
（2）请你判断谁的说法正确，为什么？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
