
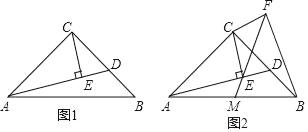
【题目】在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D是边BC上任意一点,连接AD,过点C作CE⊥AD于点E.
(1)如图1,若∠BAD=15°,且CE=1,求线段BD的长;
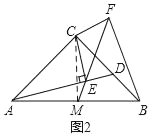
(2)如图2,过点C作CF⊥CE,且CF=CE,连接FE并延长交AB于点M,连接BF,求证:AM=BM.
【答案】(1) 2﹣![]() ;(2)见解析
;(2)见解析
【解析】分析:(1)先求得:∠CAE=45°-15°=30°,根据直角三角形30°角的性质可得AC=2CE=2,再得∠ECD=90°-60°=30°,设ED=x,则CD=2x,利用勾股定理得:![]() x=1,求得x的值,可得BD的长;
x=1,求得x的值,可得BD的长;
(2)如图2,连接CM,先证明△ACE≌△BCF,则∠BFC=∠AEC=90°,证明C、M、B、F四点共圆,则∠BCM=∠MFB=45°,由等腰三角形三线合一的性质可得AM=BM.
详解:(1)∵∠ACB=90°,AC=BC,
∴∠CAB=45°,
∵∠BAD=15°,
∴∠CAE=45°﹣15°=30°,
Rt△ACE中,CE=1,
∴AC=2CE=2,
Rt△CED中,∠ECD=90°﹣60°=30°,
∴CD=2ED,
设ED=x,则CD=2x,
∴CE=![]() x,
x,
∴![]() x=1,
x=1,
x=![]() ,
,
∴CD=2x=![]() ,
,
∴BD=BC﹣CD=AC﹣CD=2﹣![]() ;
;
(2)如图2,连接CM,
∵∠ACB=∠ECF=90°,
∴∠ACE=∠BCF,
∵AC=BC,CE=CF,
∴△ACE≌△BCF,
∴∠BFC=∠AEC=90°,
∵∠CFE=45°,
∴∠MFB=45°,
∵∠CFM=∠CBA=45°,
∴C、M、B、F四点共圆,
∴∠BCM=∠MFB=45°,
∴∠ACM=∠BCM=45°,
∵AC=BC,
∴AM=BM.


科目:初中数学 来源: 题型:
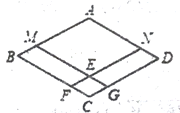
【题目】已知,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E;
(1)如图,求证:四边形AMEN是菱形;
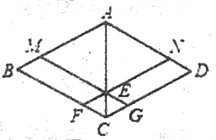
(2)如图,连接AC,在不添加任何辅助线的情况下,请直接写出面积相等的四边形;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】C点的坐标为(4,4),A为y轴负半轴上一动点,连CA,CB⊥CA交x轴于B.
(1)求OB﹣OA的值;
(2)E在x轴正半轴上,D在y轴负半轴上,∠DCE=45°,转动∠DCE,求线段BE、DE和AD之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD中,E为BC边上一点,且AE交DC延长线于F,连接BF,下列关于面积的结论中错误的是( )
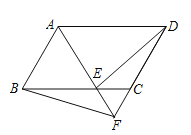
A.S△ABF =S△ADEB.S△ABF =S△ADF
C.S△ABF=![]() S□ABCDD.S△ADE=
S□ABCDD.S△ADE=![]() S□ABCD
S□ABCD
查看答案和解析>>
科目:初中数学 来源: 题型:
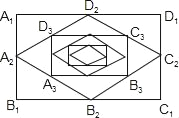
【题目】如图:顺次连接矩形A1B1C1D1四边的中点得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点得四边形A3B3C3D3,…,按此规律得到四边形AnBnCnDn.若矩形A1B1C1D1的面积为24,那么四边形AnBnCnDn的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
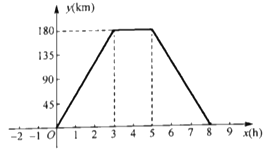
【题目】某物流公司的快递车和货车每天沿同一条路线往返于A、B两地,快递车比货车多往返一趟.如图所示,表示货车距离A地的路程y(单位:h)与所用时间x(单位h)的图像,其间在B地装卸货物2h.已知快递车比货车早1h出发,最后一次返回A地比货车晚1h.若快递车往返途中速度不变,且在A、B两地均不停留,则两车在往返途中相遇的次数为________次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店出售书包和文具盒,书包每个定价30元,文具盒每个定价5元.该店制定了两种优惠方案.
方案1:买一个书包赠送一个文具盒;
方案2:按总价的9折(总价的90%)付款.
某班学生需购买8个书包,文具盒若干(不少于8个),如果设文具盒数为x(个),付款数为y(元).
(1)分别求出两种优惠方案中y与x之间的关系式;
(2)购买文具盒多少个时两种方案付款相同;购买文具盒数大于8个时,两种方案中哪一种更省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com