
【题目】C点的坐标为(4,4),A为y轴负半轴上一动点,连CA,CB⊥CA交x轴于B.
(1)求OB﹣OA的值;
(2)E在x轴正半轴上,D在y轴负半轴上,∠DCE=45°,转动∠DCE,求线段BE、DE和AD之间的数量关系.
【答案】(1)8;(2)①当D在OA的延长线上时,DE=AD+BE;②当D在边OA上时,DE=BE﹣AD
【解析】
(1)如图1,作辅助线,证明△CQA≌△CPB(AAS),可得PB=AQ,根据线段的和与差可得结论;
(2)存在两种情况:
①当D在OA的延长线上时,如图2,作辅助线,证明△CAD≌△CBM(ASA)和△DCE≌△MCE(SAS),得DE=EM,AD=BM,相加可得结论.
②当D在边OA上时,如图3,同理可得;DE=BE-AD.
解:(1)如图1,过C作CQ⊥y轴于Q,过C作CP⊥OB于P,
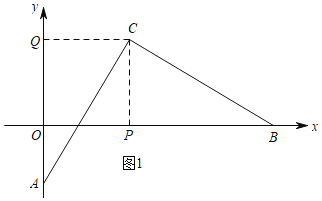
∵C(4,4),
∴CQ=CP=OQ=OP=4,
∵AC⊥BC,
∴∠ACB=∠ACP+∠BCP=∠BCP+∠PBC=90°,
∴∠ACP=∠PBC,
∵OA∥PC,
∴∠CAQ=∠ACP=∠PBC,
∵∠CPB=∠CQA=90°,
∴△CQA≌△CPB(AAS),
∴PB=AQ,
∴OB﹣OA=OP+PB﹣OA=OP+AQ﹣OA=OP+OQ=8;
(2)分两种情况:
①当D在OA的延长线上时,DE=AD+BE,理由是:
如图2,过C作CM⊥CD,交x轴于M,
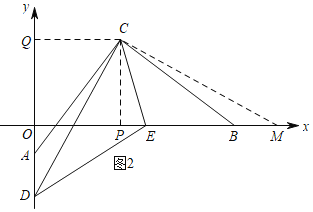
∵AC⊥BC,
∴∠ACD=∠BCM,
由(1)知:△CQA≌△CPB,
∴AC=BC,∠CAQ=∠PBC,
∴∠DAC=∠MBC,
∴△CAD≌△CBM(ASA),
∴BM=AD,CD=CM,
∵∠ACB=90°,∠DCE=45°,
∴∠ACD+∠BCE=45°=∠BCM+∠BCE=∠ECM,
∵CE=CE,
∴△DCE≌△MCE(SAS),
∴DE=EM,
∴EM=BE+BM=BE+AD=DE,
即DE=AD+BE.
②当D在边OA上时,DE=BE﹣AD,理由是:
如图3,过C作CM⊥CD,交x轴于M,
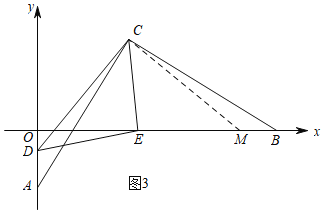
同理得△CAD≌△CBM(ASA),
∴BM=AD,CD=CM,
同理得:△DCE≌△MCE(SAS),
∴DE=EM,
∴EM=BE﹣BM=BE﹣AD=DE,
即DE=BE﹣AD.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
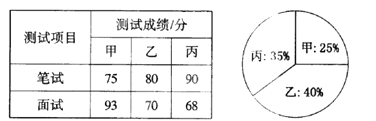
根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如上图所示,每得一票记作1分.
(l)请算出三人的民主评议得分;
(2)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确到 0.01 )?
(3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按 4 : 3 : 3 的比例确定个人成绩,那么谁将被录用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
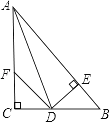
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
求证:(1)CF=EB.
(2)AB=AF+2EB.
查看答案和解析>>
科目:初中数学 来源: 题型:
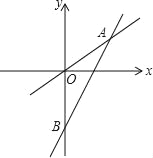
【题目】如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB.
(1)求这两个函数的解析式;
(2)求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
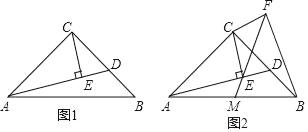
【题目】在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D是边BC上任意一点,连接AD,过点C作CE⊥AD于点E.
(1)如图1,若∠BAD=15°,且CE=1,求线段BD的长;
(2)如图2,过点C作CF⊥CE,且CF=CE,连接FE并延长交AB于点M,连接BF,求证:AM=BM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 绕点A旋转
绕点A旋转![]() 得到
得到![]() ,
,
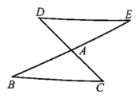
(1)则DE与BC的位置关系是_________,数量关系是_________;
(2)若![]() ,则
,则![]() _________;
_________;
(3)若![]() ,
,![]() ,
,![]() 的周长为偶数,则AE的长为_________;
的周长为偶数,则AE的长为_________;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com