
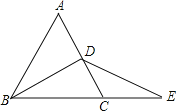
【题目】已知△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD=1,连接DE,求DE的长.
【答案】DE=![]()
【解析】
根据等边三角形的性质可得∠ABC=∠ACB=60°,AC=BC,∠DBC=![]() ∠ABC=30°,∠BDC=90°,AD=CD=
∠ABC=30°,∠BDC=90°,AD=CD=![]() AC,再证明∠E=30°=∠DBC,根据等腰三角形的性质可得BD=DE,在Rt△BDC中,BC=2,CD=1,根据勾股定理求得BD=
AC,再证明∠E=30°=∠DBC,根据等腰三角形的性质可得BD=DE,在Rt△BDC中,BC=2,CD=1,根据勾股定理求得BD=![]() ,即可求得DE=
,即可求得DE=![]() .
.
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,AC=BC,
∵BD为中线,
∴∠DBC=![]() ∠ABC=30°,∠BDC=90°,AD=CD=
∠ABC=30°,∠BDC=90°,AD=CD=![]() AC,
AC,
∵CD=CE=1,
∴∠E=∠CDE,AC=BC=2,
∵∠E+∠CDE=∠ACB=60°,
∴∠E=30°=∠DBC,
∴BD=DE,
在Rt△BDC中,BC=2,CD=1,
根据勾股定理求得BD=![]() ,
,
∴DE=BD=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某中学库存若干套桌椅,准备修理后支援贫困山区学校。现有甲、乙两木工组,甲每天修理桌椅16套,乙每天修桌椅比甲多8套,甲单独修完这些桌椅比乙单独修完多用20天,学校每天付甲组80元修理费,付乙组120元修理费。
(1)该中学库存多少套桌椅?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:a、由甲单独修理;b、由乙单独修理;c、甲、乙合作同时修理。你认为哪种方案省时又省钱?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】C点的坐标为(4,4),A为y轴负半轴上一动点,连CA,CB⊥CA交x轴于B.
(1)求OB﹣OA的值;
(2)E在x轴正半轴上,D在y轴负半轴上,∠DCE=45°,转动∠DCE,求线段BE、DE和AD之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
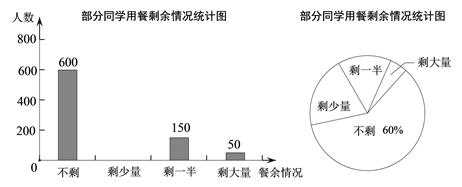
(1)这次被调查的同学共有 人;
(2)补全条形统计图,并在图上标明相应的数据;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD中,E为BC边上一点,且AE交DC延长线于F,连接BF,下列关于面积的结论中错误的是( )
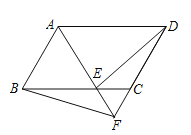
A.S△ABF =S△ADEB.S△ABF =S△ADF
C.S△ABF=![]() S□ABCDD.S△ADE=
S□ABCDD.S△ADE=![]() S□ABCD
S□ABCD
查看答案和解析>>
科目:初中数学 来源: 题型:
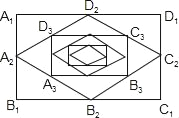
【题目】如图:顺次连接矩形A1B1C1D1四边的中点得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点得四边形A3B3C3D3,…,按此规律得到四边形AnBnCnDn.若矩形A1B1C1D1的面积为24,那么四边形AnBnCnDn的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店出售书包和文具盒,书包每个定价30元,文具盒每个定价5元.该店制定了两种优惠方案.
方案1:买一个书包赠送一个文具盒;
方案2:按总价的9折(总价的90%)付款.
某班学生需购买8个书包,文具盒若干(不少于8个),如果设文具盒数为x(个),付款数为y(元).
(1)分别求出两种优惠方案中y与x之间的关系式;
(2)购买文具盒多少个时两种方案付款相同;购买文具盒数大于8个时,两种方案中哪一种更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
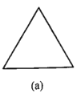
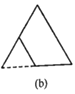
【题目】如图所示,图(a)是一块边长为1,周长记为![]() 的正三角形纸板,沿图(a)的底边剪去一块边长为
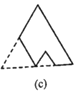
的正三角形纸板,沿图(a)的底边剪去一块边长为![]() 的正三角形纸板后得到图(b),然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的
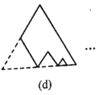
的正三角形纸板后得到图(b),然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的![]() 后,得图(c),(d),……,记第
后,得图(c),(d),……,记第![]() )块纸板的周长为Pn.则
)块纸板的周长为Pn.则![]() ____;
____;![]() _______.
_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com