
【题目】如图,![]() 的面积为
的面积为![]() ,
,![]() 、
、![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]()
![]() .连接
.连接![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() .则四边形
.则四边形![]() 的面积为_____.
的面积为_____.
【答案】![]() .
.
【解析】
先画出图形,再作DJ∥EC交AB于J,交AH于K,作DG∥BC交AH于G.由题推出EF:FC=1:3,BH:CH=1:2,求出△BEF,△BFH的面积即可.
根据题意画出图形:
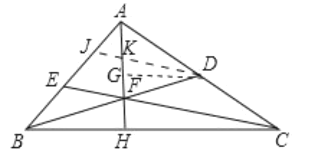
作DJ∥EC交AB于J,交AH于K作DG∥BC交AH于G.
∵DJ∥EC,AD=DC,
∴AJ=JE,AK=KF,
∴EF=2JK,DJ=2EF,CF=2DK,
设JK=m,则EF=2m,DJ=4m,DK=3m,CF=6m,
∴EF:CF=1:3,
∵AE= 2BE,
∴BE=EJ,
∵EF∥DJ,
∴BF=DF,
∵GD∥BH,
∴∠GDF=∠FBH,
∵∠GFD=∠HFB,BF=DF,
∴△DFG≌△BFH(ASA),
∴DG=BH,
∵DG∥CH,AD=DC,
∴AG=GH,
∴CH=2DG,
∴BH=2CH,
∵BE=![]() AB,
AB,
∴S△BEC=![]() S△ABC=
S△ABC=![]() ,
,
∵EG=![]() EC,
EC,
∴S△BEF=![]() S△BEC=
S△BEC=![]() ,S△BFC=
,S△BFC=![]() ,
,
∵BH=![]() BC,
BC,
∴S△BHF=![]() ×
×![]() =
=![]() ,
,
∴S四边形BEFH=![]() +
+![]() =
=![]()


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
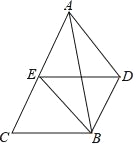
【题目】如图,已知DB∥AC,E是AC的中点,DB=AE,连结AD、BE.
(1)求证:四边形DBCE是平行四边形;
(2)若要使四边形ADBE是矩形,则△ABC应满足什么条件?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为![]() 的正方形的边长增加
的正方形的边长增加![]() ,得到一个边长为
,得到一个边长为![]() 的正方形.在图1的基础上,某同学设计了一个解释验证
的正方形.在图1的基础上,某同学设计了一个解释验证![]() 的方案(详见方案1)
的方案(详见方案1)
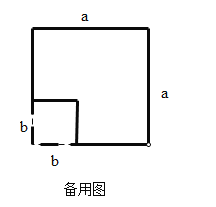
方案1.如图2,用两种不同的方式表示边长为![]() 的正方形的面积.
的正方形的面积.
方式1:![]()
方式2:![]()
因此,![]()
(1)请模仿方案1,在图1的基础上再设计一种方案,用以解释验证![]() ;
;
(2)如图3,在边长为![]() 的正方形纸片上剪掉边长为
的正方形纸片上剪掉边长为![]() 的正方形,请在此基础上再设计一个方案用以解释验证
的正方形,请在此基础上再设计一个方案用以解释验证![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
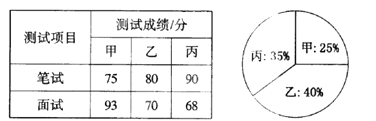
根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如上图所示,每得一票记作1分.
(l)请算出三人的民主评议得分;
(2)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确到 0.01 )?
(3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按 4 : 3 : 3 的比例确定个人成绩,那么谁将被录用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
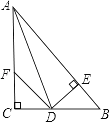
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
求证:(1)CF=EB.
(2)AB=AF+2EB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com