
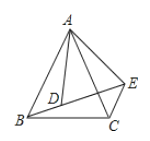
【题目】如图,已知![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 在同一直线上,则
在同一直线上,则![]() 的度数为__________.
的度数为__________.
【答案】![]()
【解析】
由已知条件可证明△ABD≌△ACE,可知∠ABD=∠ACE,在等腰△ADE中可求得∠ADE,利用外角的性质可求得∠BAD+∠ABD,在△ACE中利用三角形内角和可求得∠BEC.
∵∠BAC=∠DAE=50°,
∴∠BAD=∠CAE,
在△ABD和△ACE中
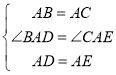
∴△ABD≌△ACE(SAS),
∴∠BAD=∠CAE,∠ABD=∠ACE,
∵AD=AE,∠DAE=50°,
∴∠ADE=∠AED=65°,
∵∠BAD+∠ABD=∠ADE,
∴∠CAE+∠ACE=∠ADE=65°,
在△ACE中,∠BEC=180°-∠AEC-(∠CAE+∠ACE)=180°-65°-65°=50°,
故答案为:50°.


科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD,∠A=60°,AB=6,点E,F分别是AB,BC边上沿某一方向运动的点,且DE=DF,当点E从A运动到B时,线段EF的中点O运动的路程为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
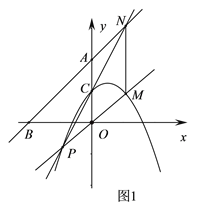
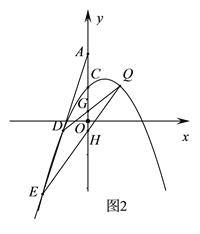
【题目】已知,抛物线y=-![]() x2 +bx+c交y轴于点C(0,2),经过点Q(2,2).直线y=x+4分别交x轴、y轴于点B、A.
x2 +bx+c交y轴于点C(0,2),经过点Q(2,2).直线y=x+4分别交x轴、y轴于点B、A.
(1)直接填写抛物线的解析式________;
(2)如图1,点P为抛物线上一动点(不与点C重合),PO交抛物线于M,PC交AB于N,连MN.
求证:MN∥y轴;
(3)如图,2,过点A的直线交抛物线于D、E,QD、QE分别交y轴于G、H.求证:CG CH为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
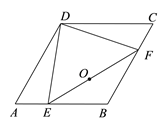
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EE⊥AB,垂足为F,连接DF;
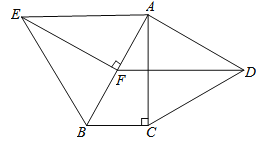
求证:(1)AC=EF;
(2)四边形ADFE是平行四边形;
(3)AC⊥DF;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若AC=9,AB=15,且S△ABC=54,则△ABD的面积是( )
MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若AC=9,AB=15,且S△ABC=54,则△ABD的面积是( )
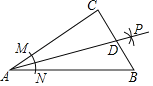
A. ![]() B.
B. ![]() C. 45D. 35
C. 45D. 35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
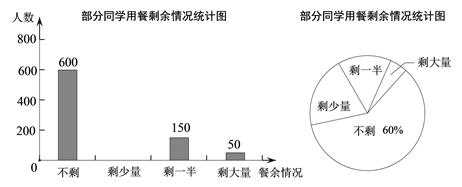
(1)这次被调查的同学共有 人;
(2)补全条形统计图,并在图上标明相应的数据;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐.
查看答案和解析>>
科目:初中数学 来源: 题型:
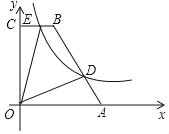
【题目】如图,在四边形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且![]() ,双曲线y=
,双曲线y=![]() (k>0)经过点D,交BC于点E
(k>0)经过点D,交BC于点E
(1)求双曲线的解析式;
(2)求四边形ODBE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com