
【题目】如图,若在△ABC 的外部作正方形 ABEF 和正方形 ACGH, 求证:△ABC 的高线 AD 平分线段 FH
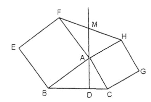
【答案】见解析.
【解析】
从H作HQ⊥AD于Q,从F作FP⊥AD于P,分别证明△ADC≌△QAH,△ABD≌△FAP得出FP=QH,证明△FMP≌△HMQ,得出FM=MH,从而得出结论.
从H作HQ⊥AD于Q,从F作FP⊥AD于P,
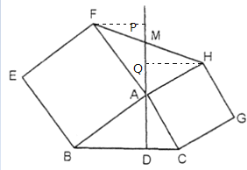
∵ACGH为正方形
∴∠QAH+∠DAC=90°, AH=AC,
∵AD为△ABC的高线
∴∠ADC=90°,∠DAC+∠DCA=90°,
∴∠QAH=∠DCA
∵HQ⊥AD
∵ ∠AQH=90°,
∴∠AQH=∠ADC
∵AH=AC,∠QAH=∠DCA,∠AQH=∠ADC
∴△ADC≌△QAH
∴QH=AD,
同理可证,△ABD≌△FAP,
∴FP=AD,
∴QH= FP,
又∵∠FPM=∠AQH=90°,∠FMP=∠QMH
∴△FMP≌△HMQ,
∴FM=MH,
∴△ABC的高线AD所在直线平分线段FH


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
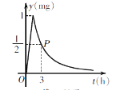
【题目】为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t之间的函数解析式为y=![]() (a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(1)写出从释放药物开始,y与t之间的两个函数解析式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么药物释放开始,至少需要经过多少小时,学生才能进入教室?
查看答案和解析>>
科目:初中数学 来源: 题型:
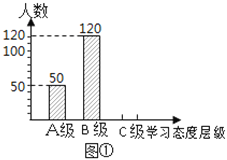
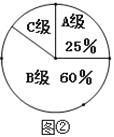
【题目】某市教育局对该市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了________名学生;
(2)图②中C级所占的圆心角的度数是__________;
(3)根据抽样调查结果,请你估计该市近20000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元一次方程组解答此问题.
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.1.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)2.请问至少需要补充多少名新工人才能在规定期内完成总任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.

【答案】(1)v=![]() (2<t≤5) (2)8米/分
(2<t≤5) (2)8米/分
【解析】分析:(1)由图象可知前一分钟过点(1,2),后三分钟时过点(2,8),分别利用待定系数法可求得函数解析式;
(2)把t=2代入(1)中二次函数解析式即可.
详解:(1)v=at2的图象经过点(1,2),
∴a=2.
∴二次函数的解析式为:v=2t2,(0≤t≤2);
设反比例函数的解析式为v=![]() ,
,
由题意知,图象经过点(2,8),
∴k=16,
∴反比例函数的解析式为v=![]() (2<t≤5);
(2<t≤5);
(2)∵二次函数v=2t2,(0≤t≤2)的图象开口向上,对称轴为y轴,
∴弹珠在轨道上行驶的最大速度在2秒末,为8米/分.
点睛:本题考查了反比例函数和二次函数的应用.解题的关键是从图中得到关键性的信息:自变量的取值范围和图象所经过的点的坐标.
【题型】解答题
【结束】
24
【题目】阅读材料:小胖同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组旋转全等的三角形.小胖把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小胖发现若∠BAC=∠DAE,AB=AC,AD=AE,则BD=CE.
(1)在图1中证明小胖的发现;
借助小胖同学总结规律,构造“手拉手”图形来解答下面的问题:
(2)如图2,AB=BC,∠ABC=∠BDC=60°,求证:AD+CD=BD;
(3)如图3,在△ABC中,AB=AC,∠BAC=m°,点E为△ABC外一点,点D为BC中点,∠EBC=∠ACF,ED⊥FD,求∠EAF的度数(用含有m的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知A(0,a)、B(b, 0),且a、b满足: ![]() ,点D为x正半轴上一动点
,点D为x正半轴上一动点
(1)求A、B两点的坐标
(2)如图,∠ADO的平分线交y轴于点C,点 F为线段OD上一动点,过点F作CD的平行线交y轴于点H,且∠AFH=45°, 判断线段AH、FD、AD三者的数量关系,并予以证明

(3)以AO为腰,A为顶角顶点作等腰△ADO,若∠DBA=30°,直接写出∠DAO的度数

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,双曲线![]() 和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.
和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.
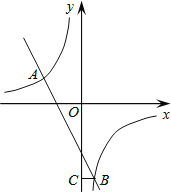
(1)求双曲线和直线的解析式;
(2)直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com