
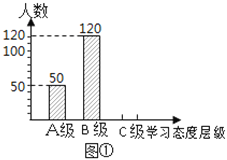
【题目】某市教育局对该市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了________名学生;
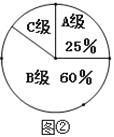
(2)图②中C级所占的圆心角的度数是__________;
(3)根据抽样调查结果,请你估计该市近20000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则以下四个结论中: ①△BDE是等边三角形; ②AE∥BC; ③△ADE的周长是9; ④∠ADE=∠BDC.其中正确的序号是( )
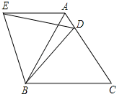
A.②③④B.①②④C.①②③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
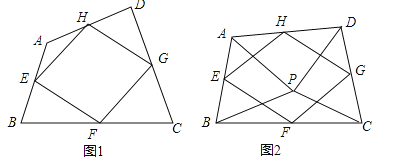
(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发部某一玩具价格如图所示,现有甲、乙两个商店,计划在“六一”儿童节前到该批发部购买此类玩具.两商店所需玩具总数为120个,乙商店所需数量不超过50个,设甲商店购买![]() 个.如果甲、乙两商店分别购买玩具,两商店需付款总和为y元.
个.如果甲、乙两商店分别购买玩具,两商店需付款总和为y元.
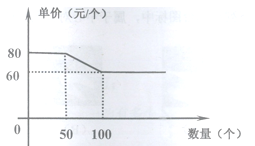
(1)求y关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若甲商店购买不超过100个,请说明甲、乙两商店联合购买比分别购买最多可节约多少钱;
(3)“六一”儿童节之后,该批发部对此玩具价格作了如下调整:数量不超过100个时,价格不变;数量超过100个时,每个玩具降价a元.在(2)的条件下,若甲、乙两商店“六一”儿童节之后去批发玩具,最多可节约2800元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE
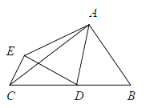
(1)求证:AD=ED
(2)连接BE,猜想△BEC的形状,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=-![]() x2 +bx+c交y轴于点C(0,2),经过点Q(2,2).直线y=x+4分别交x轴、y轴于点B、A.
x2 +bx+c交y轴于点C(0,2),经过点Q(2,2).直线y=x+4分别交x轴、y轴于点B、A.
(1)直接填写抛物线的解析式________;
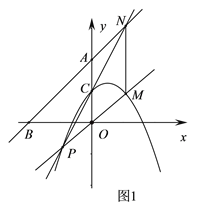
(2)如图1,点P为抛物线上一动点(不与点C重合),PO交抛物线于M,PC交AB于N,连MN.
求证:MN∥y轴;
(3)如图,2,过点A的直线交抛物线于D、E,QD、QE分别交y轴于G、H.求证:CG CH为定值.
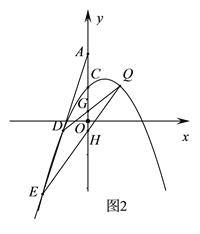
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格当中,三角形![]() 的三个顶点都在格点上.直线
的三个顶点都在格点上.直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
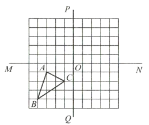
(1)画出将三角形![]() 向右平移5个单位长度后的三角形
向右平移5个单位长度后的三角形![]() (点
(点![]() 的对应点分别是点
的对应点分别是点![]() ).
).
(2)画出三角形![]() 关于直线
关于直线![]() 对称的三角形
对称的三角形![]() (点
(点![]() 的对应点分别是点
的对应点分别是点![]() ).
).
(3)画出将三角形![]() 绕着点
绕着点![]() 旋转
旋转![]() 后的三角形
后的三角形![]() (点
(点![]() 的对应点分别是点
的对应点分别是点![]() ).
).
(4)在三角形![]() ,
,![]() ,
,![]() 中,三角形 与三角形 成轴对称,三角形 与三角形 成中心对称
中,三角形 与三角形 成轴对称,三角形 与三角形 成中心对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于任意点P,给出如下定义:若⊙P的半径为1,则称⊙P为点P的“伴随圆”.
中,对于任意点P,给出如下定义:若⊙P的半径为1,则称⊙P为点P的“伴随圆”.
(1)已知,点![]() ,
,
①点![]() 在点P的“伴随圆” (填“上”或“内”或“外”);
在点P的“伴随圆” (填“上”或“内”或“外”);
②点![]() 在点P的“伴随圆” (填“上”或“内”或“外”);
在点P的“伴随圆” (填“上”或“内”或“外”);
(2)若点P在![]() 轴上,且点P的“伴随圆”与直线
轴上,且点P的“伴随圆”与直线![]() 相切,求点P的坐标;
相切,求点P的坐标;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com