
����Ŀ�����Ǹ������¶��壺˳����������һ���ı��θ����е����õ��ı��ν��е��ı��Σ�
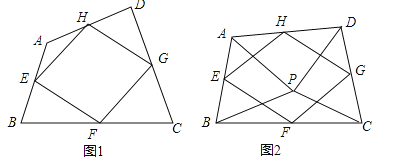
��1����ͼ1���ı���ABCD�У���E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣮��֤���е��ı���EFGH��ƽ���ı��Σ�
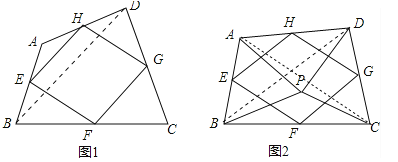
��2����ͼ2����P���ı���ABCD��һ�㣬������PA=PB��PC=PD����APB=��CPD����E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣬�����е��ı���EFGH����״����֤����IJ��룻
��3�����ı䣨2���е�������ʹ��APB=��CPD=90�㣬�����������䣬ֱ��д���е��ı���EFGH����״��������֤����
���𰸡���1��֤������������2���ı���EFGH����������3���ı���EFGH�������Σ�
��������
�����������1����ͼ1�У�����BD��������������λ�߶���ֻҪ֤��EH��FG��EH=FG���ɣ�
��2���ı���EFGH�����Σ���֤����APC�ա�BPD���õ�AC=BD����֤��EF=FG���ɣ�
��3���ı���EFGH�������Σ�ֻҪ֤����EHG=90�㣬���á�APC�ա�BPD���á�ACP=��BDP������֤����COD=��CPD=90�㣬�ٸ���ƽ���ߵ����ʼ���֤����
�����������1��֤������ͼ1�У�����BD��
�ߵ�E��H�ֱ�Ϊ��AB��DA���е㣬��EH��BD��EH=![]() BD���ߵ�F��G�ֱ�Ϊ��BC��CD���е㣬��FG��BD��FG=
BD���ߵ�F��G�ֱ�Ϊ��BC��CD���е㣬��FG��BD��FG=![]() BD����EH��FG��EH=GF�����е��ı���EFGH��ƽ���ı��Σ�
BD����EH��FG��EH=GF�����е��ı���EFGH��ƽ���ı��Σ�
��2���ı���EFGH�����Σ�
֤������ͼ2�У�����AC��BD��
�ߡ�APB=��CPD�����APB+��APD=��CPD+��APD������APC=��BPD���ڡ�APC�͡�BPD�У���AP=PB����APC=��BPD��PC=PD�����APC�ա�BPD����AC=BD���ߵ�E��F��G�ֱ�Ϊ��AB��BC��CD���е㣬��EF=![]() AC��FG=
AC��FG=![]() BD�����ı���EFGH��ƽ���ı��Σ����ı���EFGH�����Σ�
BD�����ı���EFGH��ƽ���ı��Σ����ı���EFGH�����Σ�
��3���ı���EFGH�������Σ�
֤������ͼ2�У���AC��BD���ڵ�O��AC��PD���ڵ�M��AC��EH���ڵ�N��
�ߡ�APC�ա�BPD�����ACP=��BDP���ߡ�DMO=��CMP�����COD=��CPD=90�㣬��EH��BD��AC��HG�����EHG=��ENO=��BOC=��DOC=90�㣬���ı���EFGH�����Σ����ı���EFGH�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѡ���У������෴��������� �� ��
A. ����3ǧ��������3ǧ�� B. �˽�100ǧ�����˳�180ǧ��
C. 5��������5���� D. ��������3��������7��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=��m2-3m+2��x|m|-3�Ƿ�������������m��ֵ�ǣ�������.
A.1
B.-2
C.��2
D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и������У�����ȵ�һ���ǣ�������
A. ����2��3�ͩ�23 B. ����2��2�ͩ�22
C. ����2���ͩ�2 D. |��2|3��|2|3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ж������ۺ�����״������MERS�����ڹ�״�����ƣ��������ӳ����Σ�ֱ��ԼΪ0.00000015�ף���ô0.00000015�ÿ�ѧ��������ʾΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ֱ��y=-2x+1��ͼ������ƽ��2����λ��������ƽ��1����λ�����õ�ֱ�ߵĽ���ʽ��__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ��κ���y=����x��1��2+2��ͼ������˵����ȷ���ǣ�������
A. ��x=1ʱ��y����Сֵ2 B. ��x=1ʱ��y�����ֵ2
C. ����1ʱ��y����Сֵ2 D. ��x=��1ʱ��y�����ֵ2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com