
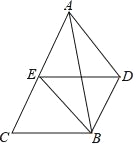
【题目】如图,已知DB∥AC,E是AC的中点,DB=AE,连结AD、BE.
(1)求证:四边形DBCE是平行四边形;
(2)若要使四边形ADBE是矩形,则△ABC应满足什么条件?说明你的理由.
【答案】(1)见解析;(2)△ABC满足AB=BC时,四边形DBEA是矩形
【解析】
(1)根据EC=BD,EC∥BD即可证明;
(2)根据等腰三角形三线合一的性质得出∠BEA=90°,根据有一个角是直角的平行四边形是矩形推出即可.
(1)∵E是AC中点,
∴AE=EC,
∵DB=AE,
∴EC=BD
又∵DB∥AC,
∴四边形DECB是平行四边形;
(2)△ABC满足AB=BC时,四边形DBEA是矩形,
理由如下:∵DB=AE,
又∵DB∥AC,
∴四边形DBEA是平行四边形(一组对边平行且相等的四边形是平行四边形),
∵AB=BC,E为AC中点,
∴∠AEB=90°,
∴平行四边形DBEA是矩形,
即△ABC满足AB=BC时,四边形DBEA是矩形.


科目:初中数学 来源: 题型:
【题目】弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如表所示.
所挂物体的质量 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
弹簧的长度 | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 |
(1)上表反映了哪些变量之间的关系?哪个是自变量,哪个是因变量?
(2)当物体的质量为2kg时,弹簧的长度是多少?
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(5)当物体的质量为2.5kg时,根据(4)的关系式,求弹簧的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若![]() ,且
,且![]() ,则我们称
,则我们称![]() 是
是![]() 的差余角.例如:若
的差余角.例如:若![]() ,则
,则![]() 的差余角
的差余角![]() .
.
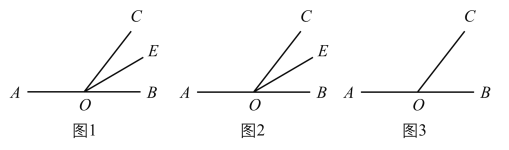
(1)如图1,点![]() 在直线
在直线![]() 上,射线
上,射线![]() 是
是![]() 的角平分线,若
的角平分线,若![]() 是
是![]() 的差余角,求
的差余角,求![]() 的度数.
的度数.
(2)如图2,点![]() 在直线
在直线![]() 上,若
上,若![]() 是
是![]() 的差余角,那么
的差余角,那么![]() 与
与![]() 有什么数量关系.
有什么数量关系.
(3)如图3,点![]() 在直线
在直线![]() 上,若
上,若![]() 是
是![]() 的差余角,且
的差余角,且![]() 与
与![]() 在直线
在直线![]() 的同侧,请你探究
的同侧,请你探究![]() 是否为定值?若是,请求出定值;若不是,请说明理由.
是否为定值?若是,请求出定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起(其中,![]() ,
,![]() ;
;![]() ).
).
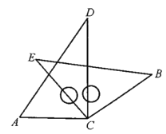
(1)①若![]() ,则
,则![]() 的度数为_____________;
的度数为_____________;
②若![]() ,则
,则![]() 的度数为_____________.
的度数为_____________.
(2)由(1)猜想![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(3)当![]() 且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出
且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出![]() 角度所有可能的值(不必说明理由);若不存在,请说明理由.
角度所有可能的值(不必说明理由);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
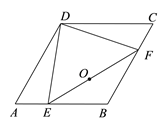
【题目】如图,菱形ABCD,∠A=60°,AB=6,点E,F分别是AB,BC边上沿某一方向运动的点,且DE=DF,当点E从A运动到B时,线段EF的中点O运动的路程为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
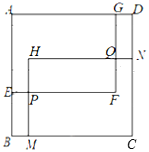
【题目】如图,在边长为6的正方形ABCD内部有两个大小相同的长方形AEFG、HMCN,HM与EF相交于点P,HN与GF相交于点Q,AG=CM=x,AE=CN=y.
(1)用含有x、y的代数式表示长方形AEFG与长方形HMCN重叠部分的面积S四边形HPFQ,并求出x应满足的条件;
(2)当AG=AE,EF=2PE时,
①AG的长为_______;
②四边形AEFG旋转后能与四边形HMCN重合,请指出该图形所在平面内能够作为旋转中心的所有点,并分别说明如何旋转的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:
垂直于同一直线的两条直线互相平行;![]() 的平方根是
的平方根是![]() ;若一个角的两边与另一个角的两边互相垂直,且其中一个角是45°,则另一个角为45°或135°;④若
;若一个角的两边与另一个角的两边互相垂直,且其中一个角是45°,则另一个角为45°或135°;④若![]() 是
是![]() 的整数部分,
的整数部分,![]() 是不等式
是不等式![]() 的最大整数解,则关于
的最大整数解,则关于![]() ,
,![]() 方程
方程![]() 的自然数解共有3对;⑤在平面直角坐标系中,点A、B的坐标分别为(2,0),(0,1),将线段AB平移至
的自然数解共有3对;⑤在平面直角坐标系中,点A、B的坐标分别为(2,0),(0,1),将线段AB平移至![]() ,
,![]() 的位置,则
的位置,则![]() .其中真命题的个数是( )
.其中真命题的个数是( )
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学库存若干套桌椅,准备修理后支援贫困山区学校。现有甲、乙两木工组,甲每天修理桌椅16套,乙每天修桌椅比甲多8套,甲单独修完这些桌椅比乙单独修完多用20天,学校每天付甲组80元修理费,付乙组120元修理费。
(1)该中学库存多少套桌椅?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:a、由甲单独修理;b、由乙单独修理;c、甲、乙合作同时修理。你认为哪种方案省时又省钱?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com