
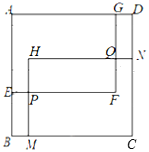
ĄŸÌâÄżĄżÈçÍŒŁŹÔڱ߳€ÎȘ6”ÄŐę·œĐÎABCDÄÚČżÓĐÁœžöŽóĐĄÏàÍŹ”Äł€·œĐÎAEFGĄąHMCNŁŹHMÓëEFÏàœ»ÓÚ”ăPŁŹHNÓëGFÏàœ»ÓÚ”ăQŁŹAG=CM=xŁŹAE=CN=yŁź
Łš1Ł©ÓĂșŹÓĐxĄąy”ÄŽúÊęÊœ±íÊŸł€·œĐÎAEFGÓ변·œĐÎHMCNÖŰ”țČż·Ö”ÄĂæ»ęSËıßĐÎHPFQŁŹČąÇółöxÓŠÂúŚă”ÄÌőŒțŁ»
Łš2Ł©”±AG=AEŁŹEF=2PEʱŁŹ
ąÙAG”Äł€ÎȘ_______Ł»
ąÚËıßĐÎAEFGĐęŚȘșóÄÜÓëËıßĐÎHMCNÖŰșÏŁŹÇëÖžłöžĂÍŒĐÎËùÔÚÆœĂæÄÚÄÜ軌śÎȘĐęŚȘÖĐĐÄ”ÄËùÓД㣏ȹ·Ö±đ˔ÜÈçșÎĐęŚȘ”ÄŁź
ĄŸŽđ°žĄżŁš1Ł©![]()
![]() ŁŹ
ŁŹ![]() Ł»Łš2Ł©ąÙ4Ł»ąÚŒûœâÎöŁź
Ł»Łš2Ł©ąÙ4Ł»ąÚŒûœâÎöŁź
ĄŸœâÎöĄż
žùŸĘŸŰĐÎșÍŐę·œĐΔÄĐÔÖÊżÉxĄąy±íÊŸłöPHĄąPF”Äł€ŁŹÀûÓĂł€·œĐÎĂæ»ęč«ÊœŒŽżÉ”Ă
Łš1Ł©ĄßAG=CM=xŁŹAE=CN=yŁŹËıßĐÎABCDÊÇŐę·œĐÎŁŹ
Ąà![]()
![]() ŁŹ
ŁŹ![]()
![]() ŁŹ
ŁŹ
Ąà![]()
![]() ŁŹ
ŁŹ![]()
![]()
ĄàÖŰ”țČż·Öł€·œĐΔÄĂæ»ęÎȘŁș![]()
![]() ŁŹ
ŁŹ
Ąßł€·œĐÎAEFGÓ변·œĐÎHMCNÓĐÖŰ”țČż·ÖŁŹŐę·œĐÎABCD±ßł€ÎȘ6ŁŹ
Ąà3<AG<6ŁŹŒŽ![]() Łź
Łź
Łš2Ł©ąÙĄßAG=AE=EFŁŹEF=2PEŁŹ
ĄàPE=![]() AGŁŹ
AGŁŹ
ĄßDG=PEŁŹAD=6ŁŹ
ĄàAD=AG+DG=AG+![]() AG=6ŁŹ
AG=6ŁŹ
œâ”ĂŁșAG=4ŁŹ
čÊŽđ°žÎȘŁș4
ąÚÈçÍŒŁŹÁŹœÓHFĄąPQŁŹÉèÏàœ»”Ä”ăÎȘ”ăOŁŹ
ĄßAG=AEŁŹEF=2PEŁŹ
ĄàËıßĐÎAEFGĄą![]() ¶ŒÊÇŐę·œĐÎŁŹ”ă
¶ŒÊÇŐę·œĐÎŁŹ”ă![]() ŒÈÊÇ
ŒÈÊÇ![]() ”ÄÖĐ”ăÒČÊÇ
”ÄÖĐ”ăÒČÊÇ![]() ”ÄÖД㣏”ă
”ÄÖД㣏”ă![]() ŒÈÊÇ
ŒÈÊÇ![]() ”ÄÖĐ”ăÒČÊÇ
”ÄÖĐ”ăÒČÊÇ![]() ”ÄÖД㣏
”ÄÖД㣏
ĄàžĂÍŒĐÎËùÔÚÆœĂæÉÏżÉÒÔŚśÎȘĐęŚȘÖĐĐĔĔăÎȘ”ă![]() Ąą”ă
Ąą”ă![]() Ąą”ă
Ąą”ă![]() ŁŹ
ŁŹ
ËıßĐÎ![]() ÈÆŚĆ”ă
ÈÆŚĆ”ă![]() ÄæʱŐë·œÏòŁš»òËłÊ±Őë·œÏòŁ©ĐęŚȘ
ÄæʱŐë·œÏòŁš»òËłÊ±Őë·œÏòŁ©ĐęŚȘ![]() ¶ÈżÉÓëËıßĐÎ
¶ÈżÉÓëËıßĐÎ![]() ÖŰșÏŁ»
ÖŰșÏŁ»
ËıßĐÎ![]() ÈÆŚĆ”ă
ÈÆŚĆ”ă![]() ËłÊ±Őë·œÏòĐęŚȘ
ËłÊ±Őë·œÏòĐęŚȘ![]() ¶ÈŁš»òÄæʱŐë·œÏòĐęŚȘ
¶ÈŁš»òÄæʱŐë·œÏòĐęŚȘ![]() ¶ÈŁ©żÉÓëËıßĐÎ
¶ÈŁ©żÉÓëËıßĐÎ![]() ÖŰșÏŁ»
ÖŰșÏŁ»
ËıßĐÎ![]() ÈÆŚĆ”ă
ÈÆŚĆ”ă![]() ÄæʱŐë·œÏòĐęŚȘ
ÄæʱŐë·œÏòĐęŚȘ![]() ¶ÈŁš»òËłÊ±Őë·œÏòĐęŚȘ
¶ÈŁš»òËłÊ±Őë·œÏòĐęŚȘ![]() ¶ÈŁ©żÉÓëËıßĐÎ
¶ÈŁ©żÉÓëËıßĐÎ![]() ÖŰșÏŁź
ÖŰșÏŁź


 ŐăœĐ¿γÌÈęÎŹÄż±êČâÆÀżÎʱÌŰŃ”Ï”ÁĐŽđ°ž
ŐăœĐ¿γÌÈęÎŹÄż±êČâÆÀżÎʱÌŰŃ”Ï”ÁĐŽđ°ž ÖÜÖÜÇćŒìČâÏ”ÁĐŽđ°ž
ÖÜÖÜÇćŒìČâÏ”ÁĐŽđ°ž ÇáÇɶáčÚÖÜČâÔÂżŒÖ±ÍšžßżŒÏ”ÁĐŽđ°ž
ÇáÇɶáčÚÖÜČâÔÂżŒÖ±ÍšžßżŒÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘËıßĐÎABCDÊÇŸŰĐÎ
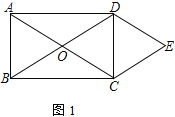

(1) ÈçÍŒ1ŁŹ¶ÔœÇÏßACĄąBDÏàœ»ÓÚ”ăOŁŹÇÒDEĄÎACŁŹCEĄÎBDŁŹÇóÖ€ŁșËıßĐÎOCEDÊÇÁâĐÎ
(2) ÈçÍŒ2ŁŹ¶ÔœÇÏßACĄąBDÏàœ»ÓÚ”ăOŁŹĄÏBAD”ÄÆœ·ÖÏßœ»BCÓÚ”ăFŁŹÇÒĄÏCAFŁœ15ĄăŁŹÇóAFĄĂFC”ÄÖ”
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
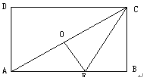
ĄŸÌâÄżĄżÈçÍŒŁŹ”ăOÊÇŸŰĐÎABCD”ÄÖĐĐÄŁŹEÊÇABÉÏ”Ä”ăŁŹŃŰCEŐÛ”țșóŁŹ”ăBÇĄșĂÓë”ăOÖŰșÏŁŹÈôBC=3ŁŹÔòŐÛșÛCE”Äł€ÎȘŁšĄĄĄĄŁ©
A. ![]() B.
B. ![]() C.
C. ![]() D. 6
D. 6
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘŁșÈçÍŒŁŹÒ»ŽÎșŻÊę![]() ”ÄÍŒÏóÓë·Ž±ÈÀęșŻÊę
”ÄÍŒÏóÓë·Ž±ÈÀęșŻÊę![]() Łš
Łš![]() Ł©”ÄÍŒÏóœ»ÓÚ”ă
Ł©”ÄÍŒÏóœ»ÓÚ”ă![]() .
.![]() ÖáÓÚ”ă
ÖáÓÚ”ă![]() ŁŹ
ŁŹ![]() ÖáÓÚ”ă
ÖáÓÚ”ă![]() . Ò»ŽÎșŻÊę”ÄÍŒÏó·Ö±đœ»
. Ò»ŽÎșŻÊę”ÄÍŒÏó·Ö±đœ»![]() Ö᥹
Ö᥹![]() ÖáÓÚ”ă
ÖáÓÚ”ă![]() Ąą”ă
Ąą”ă![]() ŁŹÇÒ
ŁŹÇÒ![]() ŁŹ
ŁŹ![]() .
.
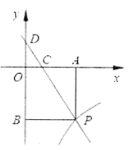
Łš1Ł©Çó”ă![]() ”ÄŚű±êŁ»
”ÄŚű±êŁ»
Łš2Ł©ÇóÒ»ŽÎșŻÊęÓë·Ž±ÈÀęșŻÊę”ÄœâÎöÊœŁ»
Łš3Ł©žùŸĘÍŒÏóĐŽłö”±![]() ÈĄșÎ֔ʱŁŹÒ»ŽÎșŻÊę”Ä֔ХÓÚ·Ž±ÈÀęșŻÊę”ÄÖ”Łż
ÈĄșÎ֔ʱŁŹÒ»ŽÎșŻÊę”Ä֔ХÓÚ·Ž±ÈÀęșŻÊę”ÄÖ”Łż
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
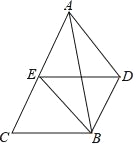
ĄŸÌâÄżĄżÈçÍŒŁŹÒŃÖȘDBĄÎACŁŹEÊÇAC”ÄÖД㣏DBŁœAEŁŹÁŹœáADĄąBEŁź
Łš1Ł©ÇóÖ€ŁșËıßĐÎDBCEÊÇÆœĐĐËıßĐÎŁ»
Łš2Ł©ÈôÒȘÊčËıßĐÎADBEÊÇŸŰĐÎŁŹÔòĄśABCÓŠÂúŚăÊČĂŽÌőŒțŁżË”ĂśÄă”ÄÀíÓÉŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÏÂÁĐË”·šÖĐŁŹŐęÈ·”ÄÊÇŁšĄĄĄĄŁ©
A.Ö±ÏßÍâÒ»”ă”œŐâÌőÖ±ÏߔĎčÏ߶ΣŹœĐŚö”ă”œÖ±ÏߔğàÀ룻
B.ÒŃÖȘÏ߶Î![]() ŁŹ
ŁŹ![]() ÖᣏÈô”ă
ÖᣏÈô”ă![]() ”ÄŚű±êÎȘŁš-1ŁŹ2Ł©ŁŹÔò”ă
”ÄŚű±êÎȘŁš-1ŁŹ2Ł©ŁŹÔò”ă![]() ”ÄŚű±êÎȘŁš-1ŁŹ-2Ł©»òŁš-1ŁŹ6Ł©Ł»
”ÄŚű±êÎȘŁš-1ŁŹ-2Ł©»òŁš-1ŁŹ6Ł©Ł»
C.Èô![]() Óë
Óë![]() »„ÎȘÏà·ŽÊ꣏Ôò
»„ÎȘÏà·ŽÊ꣏Ôò![]() Ł»
Ł»
D.ÒŃÖȘčŰÓÚ![]() ”ÄČ»”ÈÊœ
”ÄČ»”ÈÊœ![]() ”ÄœâŒŻÊÇ
”ÄœâŒŻÊÇ![]() ŁŹÔò
ŁŹÔò![]() ”ÄÈĄÖ”·¶Î§ÎȘ
”ÄÈĄÖ”·¶Î§ÎȘ![]() Łź
Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹËıßĐÎABCDÖĐŁŹĄÏABCŁœ90ĄăŁŹABŁœ4ŁŹBCŁœ3ŁŹCDŁœ12ŁŹADŁœ13ŁźÇóËıßĐÎABCD”ÄĂæ»ęŁź

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹOÊÇĄśABC”ÄÍâĐÄŁŹIÊÇĄśABC”ÄÄÚĐÄŁŹÁŹAIČąŃÓł€œ»BCșÍĄŃOÓÚDĄąEÁœ”ă.
Łš1Ł©ÇóÖ€ŁșEBŁœEIŁ»
Łš2Ł©ÈôABŁœ4ŁŹACŁœ3ŁŹBEŁœ2ŁŹÇóAI”Äł€.

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżĆŚÎïÏßy=ax2+bx+3ŁšaĄÙ0Ł©Ÿčę”ăAŁš©1ŁŹ0Ł©ŁŹBŁš![]() ŁŹ0Ł©ŁŹÇÒÓëyÖáÏàœ»ÓÚ”ăCŁź
ŁŹ0Ł©ŁŹÇÒÓëyÖáÏàœ»ÓÚ”ăCŁź
Łš1Ł©ÇóŐâÌőĆŚÎïÏߔıíŽïÊœŁ»
Łš2Ł©ÇóĄÏACB”ĶÈÊꣻ
Łš3Ł©Éè”ăDÊÇËùÇóĆŚÎïÏß”ÚÒ»ÏóÏȚÉÏÒ»”㣏ÇÒÔÚ¶ÔłÆÖá”ÄÓÒČàŁŹ”ăEÔÚÏ߶ÎACÉÏŁŹÇÒDEĄÍACŁŹ”±ĄśDCEÓ륜AOCÏàËÆʱŁŹÇó”ăD”ÄŚű±êŁź

Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com