
【题目】如图所示,![]() 绕点A旋转
绕点A旋转![]() 得到
得到![]() ,
,
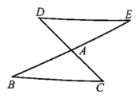
(1)则DE与BC的位置关系是_________,数量关系是_________;
(2)若![]() ,则
,则![]() _________;
_________;
(3)若![]() ,
,![]() ,
,![]() 的周长为偶数,则AE的长为_________;
的周长为偶数,则AE的长为_________;
【答案】(1)![]() ;
;![]() ;(2)24;(3)4.
;(2)24;(3)4.
【解析】
(1)根据旋转的性质可得,DE=BC,∠E=∠B,然后根据内错角相等,两直线平行即可得出结论;
(2)根据旋转的性质可得△AED≌△ABC,从而得出结论;
(3)根据旋转的性质可得AD=AC=2,ED=BC=4,然后根据三角形的周长和三边关系即可求出AE的长.
解:(1)由旋转的性质可得:DE=BC,∠E=∠B
∴![]()
故答案为:![]() ;
;![]() .
.
(2)由旋转的性质可得△AED≌△ABC,
∴![]()
![]()
故答案为:24.
(3)由旋转的性质可得AD=AC=2,ED=BC=4,
在△ADE中,ED -AD<AE<ED+AD
即2<AE<6
∵![]() 的周长为偶数,AD、ED均为偶数
的周长为偶数,AD、ED均为偶数
∴AE也为偶数
∴AE=4
故答案为:4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】C点的坐标为(4,4),A为y轴负半轴上一动点,连CA,CB⊥CA交x轴于B.
(1)求OB﹣OA的值;
(2)E在x轴正半轴上,D在y轴负半轴上,∠DCE=45°,转动∠DCE,求线段BE、DE和AD之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店出售书包和文具盒,书包每个定价30元,文具盒每个定价5元.该店制定了两种优惠方案.
方案1:买一个书包赠送一个文具盒;
方案2:按总价的9折(总价的90%)付款.
某班学生需购买8个书包,文具盒若干(不少于8个),如果设文具盒数为x(个),付款数为y(元).
(1)分别求出两种优惠方案中y与x之间的关系式;
(2)购买文具盒多少个时两种方案付款相同;购买文具盒数大于8个时,两种方案中哪一种更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地图书馆为了满足群众多样化阅读的需求,决定购买甲、乙两种品牌的电脑若干组建电子阅览室.经了解,甲、乙两种品牌的电脑单价分别3100元和4600元.
(1)若购买甲、乙两种品牌的电脑共50台,恰好支出200000元,求甲、乙两种品牌的电脑各购买了多少台?
(2)若购买甲、乙两种品牌的电脑共50台,每种品牌至少购买一台,且支出不超过160000元,共有几种购买方案?并说明哪种方案最省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,点E与点F分别在线段AC、BC上,且四边形DEFG是正方形.


(1)试探究线段AE与CG的关系,并说明理由.
(2)如图②若将条件中的四边形ABCD与四边形DEFG由正方形改为矩形,AB=3,BC=4.
①线段AE、CG在(1)中的关系仍然成立吗?若成立,请证明,若不成立,请写出你认为正确的关系,并说明理由.
②当△CDE为等腰三角形时,求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
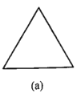
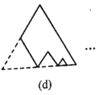
【题目】如图所示,图(a)是一块边长为1,周长记为![]() 的正三角形纸板,沿图(a)的底边剪去一块边长为
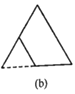
的正三角形纸板,沿图(a)的底边剪去一块边长为![]() 的正三角形纸板后得到图(b),然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的
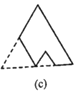
的正三角形纸板后得到图(b),然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的![]() 后,得图(c),(d),……,记第
后,得图(c),(d),……,记第![]() )块纸板的周长为Pn.则
)块纸板的周长为Pn.则![]() ____;
____;![]() _______.
_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直角梯形OABC中,BC∥OA,OA=6,BC=2,∠BAO=45°.
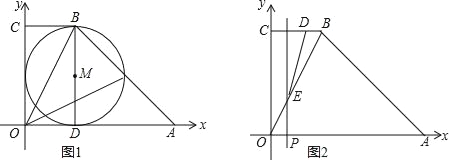
(1)OC的长为 ;
(2)D是OA上一点,以BD为直径作⊙M,⊙M交AB于点Q.当⊙M与y轴相切时,sin∠BOQ= ;
(3)如图2,动点P以每秒1个单位长度的速度,从点O沿线段OA向点A运动;同时动点D以相同的速度,从点B沿折线B﹣C﹣O向点O运动.当点P到达点A时,两点同时停止运动.过点P作直线PE∥OC,与折线O﹣B﹣A交于点E.设点P运动的时间为t(秒).求当以B、D、E为顶点的三角形是直角三角形时点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com