
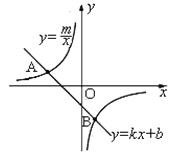
【题目】如题图,已知A(-4,2),B(n,-4)是一次函数y=kx+b的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求m,n的值;
(2)求一次函数的关系式;、
(3)结合图象直接写出一次函数小于反比例函数的x的取值范围。
科目:初中数学 来源: 题型:
【题目】一个质地均匀的小正方体,六个面分别标有数字“1”“2”“3”“4”“5”“6”. 连续两次抛掷小正方体,观察每次朝上一面的数字.
(1)请用列表格或画树状图的方法列举出两次抛掷的所有可能结果;
(2)求出第二次抛掷的数字大于第一次抛掷的数字的概率;
(3)求两次抛掷的数字之和为5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A、B两点对应的有理数分别为20和30,点P和点Q分别同时从点A和点O出发,以每秒2个单位长度,每秒4个单位长度的速度向数轴正方向运动,设运动时间为t秒. ![]()
(1)当t=2时,则P、Q两点对应的有理数分别是;PQ=;
(2)点C是数轴上点B左侧一点,其对应的数是x,且CB=2CA,求x的值;
(3)在点P和点Q出发的同时,点R以每秒8个单位长度的速度从点B出发,开始向左运动,遇到点Q后立即返回向右运动,遇到点P后立即返回向左运动,与点Q相遇后再立即返回,如此往返,直到P、Q两点相遇时,点R停止运动,求点R运动的路程一共是多少个单位长度?点R停止的位置所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A坐标为(6,0),在B在y轴的正半轴上,且S△AOB=24.
(1)求点B坐标;
(2)若点P从B出发沿y轴负半轴运动,速度每秒2个单位,运动时间t秒,△AOP的面积为S,求S与t的关系式,并直接写出t的取值范围;
(3)在(2)的条件下,若S△AOP:S△ABP=1:3,且S△AOP+S△ABP=S△AOB , 在线段AB的垂直平分线上是否存在点Q,使得△AOQ的面积与△BPQ的面积相等?若存在,求出Q点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=45°,点P在∠AOB内部,P1与P关于OB对称,P2与P关于OA对称,则P1 , O,P2三点构成的三角形是( )
A.直角三角形
B.等腰三角形
C.等边三角形
D.等腰直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com