
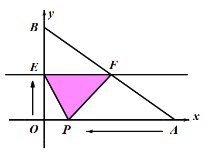
����Ŀ����ͼ����֪A��B���������ֱ�Ϊ(40��0)��(0��30)������P�ӵ�A��ʼ���߶�AO����ÿ��2����λ���ȵ��ٶ���ԭ��O�˶���ͬʱֱ��EF��x��Ϊ��ʼλ����ÿ��1����λ���ȵ��ٶ�����ƽ���ƶ�(��EF��x��)�����ҷֱ���y�ᡢ�߶�AB���ڵ�E��F������EP��FP���趯��P��ֱ��EFͬʱ�������˶�ʱ��Ϊt����
��1����t=15��ʱ����EF�ij�����
��2��ֱ��EF����P���˶����������Ƿ����������t��ʹ����PEF���������160(ƽ����λ)?���������������ʱ��ֵ��������������˵��������
���𰸡���1��EF=20����2��������ʹ��![]() ���������
���������![]() ��ƽ����λ����
��ƽ����λ����![]() ֵ.
ֵ.
��������
��1����t=15ʱ��OE=15����֤��BEF�ס�BOA����![]() ���Ӷ����EF�ij�����
���Ӷ����EF�ij�����
��2���������������t��ʹ�á�PEF���������160������������ʽ�г��������ɸ����б�ʽ�����ж����ó�������
��1����EF��OA�����BEF=��BOA��
�֡ߡ�B=��B�����BEF�ס�BOA����![]() ����t=15ʱ��OE=BE=15��OA=40��OB=30����
����t=15ʱ��OE=BE=15��OA=40��OB=30����![]() ��
��
��2���ߡ�BEF�ס�BOA����![]() ����
����![]() ����������t2��30t+240=0��
����������t2��30t+240=0��
�ߡ�=302��4��1��240=��60��0�����û��ʵ�����������ʹ�á�PEF���������160��ƽ����λ����tֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
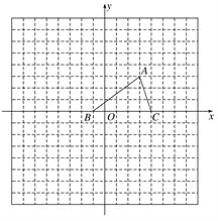
����Ŀ����ͼ����֪��ABC���������������ֱ�ΪA(3,3)��B(��1,0)��C(4,0)��
(1)����ƽ�ƣ���ʹ��ABC�Ķ���A������ԭ��O�غϣ���ֱ��д����ʱ��C�Ķ�Ӧ��C1���ꣻ(���ػ���ƽ�ƺ��������)
(2)����ABC�Ƶ�B��ʱ����ת90�㣬�õ���A��BC�䣬������A��BC�䲢д��A�������ꣻ
(3)�Ե�AΪλ�����ķŴ��ABC���õ���AB2C2��ʹ�Ŵ�ǰ������֮��Ϊ1��4�������������ڻ�����A2B2C2.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
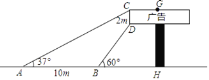
����Ŀ����ͼ�������ι���Ƽ���¥����������֪CD=2m���������õ���CAH=37�㣬��DBH=60�㣬AB=10m����GH�ij������ο����ݣ�tan37���0.75�� ![]() ��1.732�������ȷ��0.1m��
��1.732�������ȷ��0.1m��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ��߸��ϵ�C��������CE��CF�̶����߸ˣ�����CE�͵����60���ǣ�������߸�6��B�����ò���ǣ���A����õ��߸���C��������Ϊ30������֪����Ǹ�ABΪ1.5�ף�������CE�ij�������������ţ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
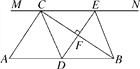
����Ŀ����ͼ����Rt��ABC�У���ACB��90�㣬AB��6������C��ֱ��MN��AB��DΪAB��һ�㣬����D��DE��BC����ֱ��MN�ڵ�E������ΪF������CD��BE.
(1)����D��AB���е�ʱ���ı���BECD��ʲô�����ı��Σ�˵��������ɣ�
(2)��(1)�������£�����A���ڶ��ٶ�ʱ���ı���BECD�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ���ļ�ʱװ������40Ԫ/�����ۼ�110Ԫ/����ÿ������20����ÿ����һ������ɵ���ƽ̨�ƹ����aԪ��a��0����δ��30�죬���ʱװ����չ��ÿ�콵��1Ԫ�����������������ӵ�1����ÿ��ĵ��۾���ǰһ�콵1Ԫ��ͨ���г����з��֣���ʱװ����ÿ��1Ԫ��ÿ����������4��������30���ڣ�Ҫʹÿ����ɵ���ƽ̨�ƹ���ú������������t��tΪ�������������������a��ȡֵ��ΧӦΪ_____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
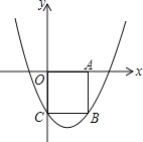
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У��߳�Ϊ2��������OABC�Ķ���A��C�ֱ���x�������ᡢy��ĸ������ϣ����κ���y��![]() (xh)2+k��ͼ��B��C���㣮
(xh)2+k��ͼ��B��C���㣮
��1����ö��κ����Ķ������ꣻ
��2����Ϻ�����ͼ��̽������y��0ʱx��ȡֵ��Χ��
��3����m��![]() ����A��m��y1����B��m+1��y2�����㶼�ڸú���ͼ���ϣ��ԱȽ�y1��y2�Ĵ�С������Ҫ˵�����ɣ�
����A��m��y1����B��m+1��y2�����㶼�ڸú���ͼ���ϣ��ԱȽ�y1��y2�Ĵ�С������Ҫ˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһƽ��ֱ������ϵ��������������y![]() ��b��0������κ���y��ax2+bx��a��0����ͼ������ǣ�������
��b��0������κ���y��ax2+bx��a��0����ͼ������ǣ�������
A.  B.
B. 
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬѧ�ǣ������ǽ�������Ժ�����ѧ���������Ǻ�����ʽ��
sin (������)��sin��cos����cos��sin����
cos (������)��cos��cos����sin��sin��
����sin 15����sin (45����30��)��sin 45��cos 30����cos 45��sin 30����![]()
(1)�Է������⣬���cos 15����ȷֵ��
(2)����֪����tan����![]() �������tan 15����ȷֵ��
�������tan 15����ȷֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com