
【题目】在△ABC中,∠A=120°,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,
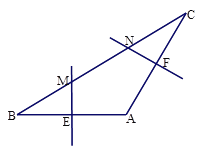
(1) 如图(1),连接AM、AN,求∠MAN的度数。
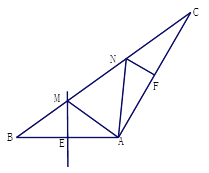
(2) 如图(2),如果AB=AC, 求证:BM=MN=NC.
【答案】(1)60 (2)见解析
【解析】试题分析:(1)由AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,根据线段垂直平分线的性质,可得AM=BM,AN=CN,继而求得∠B=∠BAM=30°,∠C=∠CAN=30°,则可求得∠MAN的大小;
(2)由∠B=∠BAM=30°,∠C=∠CAN=30°,易证得△AMN是等边三角形,则可证得BM=MN=NC.
试题解析:
(1)∠MAN=60°.
理由:∵在△ABC中,AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵ME是AB的垂直平分线,NF是AC的垂直平分线,
∴AM=BM,AN=CN,
∴∠B=∠BAM=30°,∠C=∠CAN=30°,
∴∠MAN=∠BAC-∠BAM-∠CAN=60°;
(2)证明:∵∠B=∠BAM=30°,∠C=∠CAN=30°,
∴∠AMN=∠ANM=60°,
∵∠MAN=60°,
∴△AMN是等边三角形,
∴AM=AN=MN,
∵AM=BM,AN=CN,
∴BM=MN=NC.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,四边形OABC中,OA=a,OC=5,BC=3,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处(如图1).
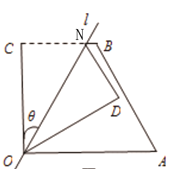
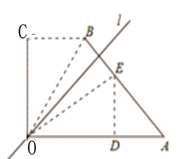
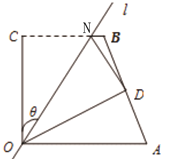
图1 图2 图3
(1)若θ=45°,四边形OABC的直角∠OCB沿直线l折叠后,点B落在点四边形OABC的边AB上 (如图2) ,求a的值. ![]()
(2)若折叠后点D恰为AB的中点(如图3),求θ的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为点D,点C的对应点为点E,连接BD,BE.
(1)如图,当α=60°时,延长BE交AD于点F.
①求证:△ABD是等边三角形;
②求证:BF⊥AD,AF=DF;
③请直接写出BE的长;
(2)在旋转过程中,过点D作DG垂直于直线AB,垂足为点G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从①∠1=∠2 ②∠C=∠D ③∠A=∠F 三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )
A.0 B.1 C.2 D.3
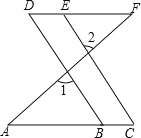
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com