
如图,有一块圆形铁皮,BC是⊙O的直径,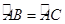 ,在此圆形铁皮中剪下一个扇形(阴影部分).
,在此圆形铁皮中剪下一个扇形(阴影部分).
(1)当⊙O的半径为2时,求这个扇形(阴影部分)的面积(结果保留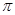 );
);
(2)当⊙O的半径为R(R>0)时,在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形
围成一个圆锥?请说明理由.
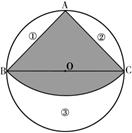
连接AO并延长交扇形、圆于点E、F

∵BC是⊙O的直径,∴∠BAC=90°
 ∵
∵  ∴AB=AC,
∴AB=AC,
∵AO=BO ∴AF⊥BC
(1)当⊙O的半径为2时:AC=AB=2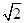
∴S阴影= ;
;
(2)当⊙O的半径为R(R>0)时:AC=AB=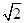 R
R
阴影部分扇形的弧长为: πR
πR
EF=2R-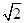 R,以EF为直径作圆,是剩余材料中所作的最大的圆,其圆周长为:(2-
R,以EF为直径作圆,是剩余材料中所作的最大的圆,其圆周长为:(2-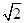 )πR
)πR
∵ πR>(2-
πR>(2-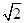 )πR
)πR
∴不能从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥.
【解析】(1)先由圆的性质求得阴影部分扇形的半径,由直径所对的圆周角是90°可知圆心角的度数,可求得阴影部分的面积;
(2)先分别用R表示出阴影部分扇形的弧长,即所要围成的圆锥的底面周长为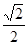 Rπ,以EF为直径作圆,是剩余材料中所作的最大的圆,求出其周长为(2-
Rπ,以EF为直径作圆,是剩余材料中所作的最大的圆,求出其周长为(2- )Rπ,比较大小可知不能从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥.
)Rπ,比较大小可知不能从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
 |
| AB |
 |
| AC |
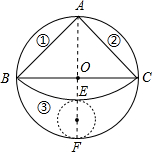 部分).
部分).查看答案和解析>>
科目:初中数学 来源:2012届江苏省南京市江宁区九年级中考二模数学试卷(带解析) 题型:解答题
如图,有一块圆形铁皮,BC是⊙O的直径,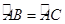 ,在此圆形铁皮中剪下一个扇形(阴影部分).
,在此圆形铁皮中剪下一个扇形(阴影部分).
(1)当⊙O的半径为2时,求这个扇形(阴影部分)的面积(结果保留 );
);
(2)当⊙O的半径为R(R>0)时,在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形
围成一个圆锥?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 =
= ,在此圆形铁皮中剪下一个扇形(阴影
,在此圆形铁皮中剪下一个扇形(阴影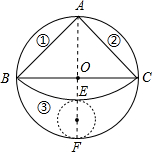 部分).
部分).查看答案和解析>>
科目:初中数学 来源:2012年江苏省南京市江宁区中考数学二模试卷(解析版) 题型:解答题
 =
= ,在此圆形铁皮中剪下一个扇形(阴影部分).
,在此圆形铁皮中剪下一个扇形(阴影部分).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com