练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    设x，y是有理数，并且x，y满足等式x2＋2y＋y＝17－4，求x＋y的值．

    答案：
    解析：

    　　解：∵x2＋2y＋y·＝17－4，

    　　∴(x2＋2y－17)＋(y＋4) ＝0，

    　　又∵x，y都是有理数，

    　　∴x2＋2y－17和y＋4都是有理数，

    　　而由于0是有理数，∴(y＋4)·必为有理数．

    　　∴∴

    　　∴当x＝5时，x＋y＝1；

    　　当x＝－5时，x＋y＝－9．


    提示：

    点悟：利用实数等于零的条件，即有理数部分和无理数部分分别是零．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知：m，n是两个连续自然数（m＜n），且q=mn．设p=
    		q+n
    +
    		q-m
    ，则p（
     
    ）．
    A、总是奇数；B、总是偶数；C、有时是奇数，有时是偶数；D、有时是有理数，有时是无理数．
    请选出答案，并给出证明过程．

    查看答案和解析>>

    科目：初中数学 来源：走进数学世界七年级（上） 题型：044

    设a、b是有理数，1＜a＜2，－1＜b＜0．在数轴上画出满足条件的一对数a、b所对应的点．再分别画出表示、－a、三数的点的大致位置，并简述理由．然后据此将上述5个有理数按从小到大的顺序排列，用小于号连接起来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

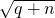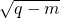    已知：m，n是两个连续自然数（m＜n），且q=mn．设p=数学公式+数学公式，则p（________）．
    A、总是奇数；B、总是偶数；C、有时是奇数，有时是偶数；D、有时是有理数，有时是无理数．
    请选出答案，并给出证明过程．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    已知：m，n是两个连续自然数（m＜n），且q=mn．设p=
    		q+n
    +
    		q-m
    ，则p（______）．
    A、总是奇数；B、总是偶数；C、有时是奇数，有时是偶数；D、有时是有理数，有时是无理数．
    请选出答案，并给出证明过程．

    查看答案和解析>>

    科目：初中数学 来源：2008-2009学年安徽省芜湖市南陵县实验初中九年级（上）第一次月考数学试卷（解析版） 题型：解答题

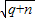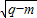    已知：m，n是两个连续自然数（m＜n），且q=mn．设p=+，则p（______）．
    A、总是奇数；B、总是偶数；C、有时是奇数，有时是偶数；D、有时是有理数，有时是无理数．
    请选出答案，并给出证明过程．

    查看答案和解析>>

    同步练习册答案