
分析 (1)首先利用十字相乘法把分子分母分解因式,再约去公因式x-9即可;
(2)首先利用分组分解法分解分子,用公式法分解分母,再约去公因式即可;
(3)首先利用平方差公式分解分母然后约去分子分母的公因式;
(4)利用十字相乘法把分母分解因式,利用完全平方公式分解分子,再约去分子分母的公因式.
解答 解:(1)原式=$\frac{x(x+3)(x-9)}{(x+1)(x-9)}$=$\frac{{{x^2}+3x}}{x+1}$;
(2)原式=$\frac{{x}^{2}(x-1)-(x-1)}{(x-1)^{2}}$=$\frac{(x-1)({x}^{2}-1)}{(x-1)^{2}}$=$\frac{(x-1)(x-1)(x+1)}{(x-1)^{2}}$=x+1;
(3)原式=$\frac{{x}^{n}+3{y}^{n}}{({x}^{n}+3{y}^{n})({x}^{n}-3{y}^{n})}$=$\frac{1}{{{x^n}-3{y^n}}}$;
(4)原式=$\frac{({x}^{2}-3)^{2}}{({x}^{2}-3)({x}^{2}+1)}$=$\frac{{{x^2}-3}}{{{x^2}+1}}$.
点评 此题主要考查了分式的约分,首先将分子、分母转化为乘积的形式,再找出分子、分母的最大公因式并约去,注意不要忽视数字系数的约分.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
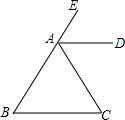 如图,已知:AD平分∠CAE,AD∥BC.
如图,已知:AD平分∠CAE,AD∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
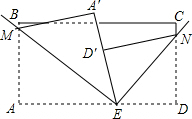 如图,长方形纸片ABCD,点E为AD边上的点,将纸片先沿直线EM对折,对折后的点A的对应点为A′,再沿直线EN对阵,对折后点D的对应点为D′,并且D′刚好落在A′E边上.
如图,长方形纸片ABCD,点E为AD边上的点,将纸片先沿直线EM对折,对折后的点A的对应点为A′,再沿直线EN对阵,对折后点D的对应点为D′,并且D′刚好落在A′E边上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com