
����Ŀ����ͼ,��Rt��ABC��,��C=90,AC=6,BC=8,����P�ӵ�A��ʼ,�ر�AC���C��ÿ��1����λ���ȵ��ٶ��˶�,����D�ӵ�A��ʼ,�ر�AB���B��ÿ��![]() ����λ���ȵ��ٶ��˶�,��ǡ����ʼ�ձ��������������ֱ��PD��AC,����Q�ӵ�C��ʼ,�ر�CB���B��ÿ��2����λ���ȵ��ٶ��˶�,����PQ.��P,D,Q�ֱ�ӵ�A,Cͬʱ����,������һ�㵽��˵�ʱ,��������Ҳ��ֹ֮ͣ�˶�,���˶�ʱ��Ϊt��(t��0).
����λ���ȵ��ٶ��˶�,��ǡ����ʼ�ձ��������������ֱ��PD��AC,����Q�ӵ�C��ʼ,�ر�CB���B��ÿ��2����λ���ȵ��ٶ��˶�,����PQ.��P,D,Q�ֱ�ӵ�A,Cͬʱ����,������һ�㵽��˵�ʱ,��������Ҳ��ֹ֮ͣ�˶�,���˶�ʱ��Ϊt��(t��0).
(1)��tΪ��ֵʱ,�ı���BQPD�����Ϊ��ABC�����![]() ?
?
(2)�Ƿ����t��ֵ��ʹ�ı���PDBQΪƽ���ı���?�����ڣ����t��ֵ���������ڣ�˵�����ɣ�
(3)�Ƿ����t��ֵ,ʹ�ı���PDBQΪ����?������,���t��ֵ;��������,˵������,��̽����θı��Q���ٶ�(�����˶�)��ʹ�ı���PDBQ��ijһʱ��Ϊ���Σ����Q���ٶȡ�

���𰸡���1��![]() ����2�����ڣ�
����2�����ڣ�![]() ����3�������ڣ�����Q���ٶ�Ϊÿ��
����3�������ڣ�����Q���ٶ�Ϊÿ��![]() ����λ����ʱ������
����λ����ʱ������![]() �룬�ı���PDBQ������.
�룬�ı���PDBQ������.
��������
(1)���ȱ�ʾ���ı�������Լ����������������з�����⼴�ɣ�
(2)��BQ//DP���ɵõ�BQ=DPʱ���ı���PDBQ��ƽ���ı��Σ��ɴ˿ɵù���t�ķ��̣��ⷽ�̼��ɵã�
(3)����(2)����������ô�ʱDP��BD�ij�����DP��BD�����ж�ƽ���ı���PDBQ����Ϊ���Σ�Ȼ�����Q���ٶ�Ϊÿ��v����λ���ȣ���Ҫʹ�ı���PDBQΪ���Σ���PD=BD=BQ���з�����⼴��.
(1)��ֱ��PD��AC��
���APD=90����
�֡ߡ�C=90����
���C=��APD��
��PD//BC��
��Rt��APD��AD=![]() ��AP=t��
��AP=t��
��PD=![]() ��PC=AC-AP=6-t��
��PC=AC-AP=6-t��
��CQ=2t��BC=8��
��BQ=8-2t��
���ı���BQPD�����Ϊ��![]() (BQ+DP)��PC=
(BQ+DP)��PC=![]() (8-2t+
(8-2t+![]() t)(6-t)��
t)(6-t)��
��ABC�������![]() ACBC=
ACBC=![]() ��6��8=24��
��6��8=24��
���ı���BQPD�����Ϊ��ABC�����![]() ʱ��
ʱ��![]() ��24=
��24=![]() (8-2t+
(8-2t+![]() t)(6-t)��
t)(6-t)��
��ã�![]() ��
��
�ߵ�����һ�㵽��˵�ʱ����������Ҳ��ֹ֮ͣ�˶���
��t��4��
��![]() �������⣬��ȥ��
�������⣬��ȥ��
�൱tΪ![]() ʱ���ı���BQPD�����Ϊ��ABC�����
ʱ���ı���BQPD�����Ϊ��ABC�����![]() ��
��
(2)���ڣ�
��PD//BC��
��BQ//DP��
�൱BQ=DPʱ���ı���PDBQ�����ı��Σ�
��8-2t=![]() ����ã�t=
����ã�t=![]() ��
��
����ڣ�t=![]() ʱ���ı���PDBQΪƽ���ı��Σ�
ʱ���ı���PDBQΪƽ���ı��Σ�
(3)�����ڣ��������£�
��![]() ʱ��
ʱ��![]() ��
��
��DP��BD��
��ƽ���ı���PDBQ����Ϊ���Σ�
���Q���ٶ�Ϊÿ��v����λ���ȣ�
��BQ=8-vt��PD=![]() ��BD=10-
��BD=10-![]() ��
��
Ҫʹ�ı���PDBQ��Ϊ���Σ���PD=BD=BQ��
��PD=BDʱ����![]() ����ã�t=
����ã�t=![]() ��
��
��PD=BQ��t=![]() ʱ����
ʱ����![]() ����ã�v=
����ã�v=![]() ��
��
���Ե���Q���ٶ�Ϊÿ��![]() ����λ����ʱ������
����λ����ʱ������![]() �룬�ı���PDBQ������.
�룬�ı���PDBQ������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A(n��-2)��B(1��4)��һ�κ���y=kx+b��ͼ��ͷ���������y=![]() ��ͼ����������㣬ֱ��AB��y�ύ�ڵ�C��
��ͼ����������㣬ֱ��AB��y�ύ�ڵ�C��
(1)����������һ�κ����Ĺ�ϵʽ��
(2)����AOC�������
(3)��ʽkx+b-![]() <0�Ľ⼯(ֱ��д����)��
<0�Ľ⼯(ֱ��д����)��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��ڴ����ڼ���Żݴ�������̳���29Ӣ���25Ӣ��ʵ繲96̨�ֱ���8�ۺ�7�۳��ۣ�����168400Ԫ����֪29Ӣ��ʵ�ԭ��Ϊ3000Ԫ/̨��25Ӣ��ʵ�ԭ��Ϊ2000Ԫ/̨������29Ӣ���25Ӣ��ʵ������̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Rt��ABC�У���BAC=90�㣬AB=3��AC=4��PΪ��BC��һ���㣬PE��AB��E��PF��AC��F��MΪEF�е㣬��AM����СֵΪ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ԲOΪԲ�ģ��뾶Ϊ1�Ļ�����������A��B���㣬P�ǻ�![]() ��һ�㣨����A��B�غϣ�������OP�����POB=�������P��������
��һ�㣨����A��B�غϣ�������OP�����POB=�������P��������

A. ��sin����sin���� B. ��cos����cos���� C. ��cos����sin���� D. ��sin����cos����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���������֣�
��ͼ���ھ���ABCD�У�E��BC���е㣬����ABE��AE�۵���õ���AFE����F�ھ���ABCD�ڲ����ӳ�AF��CD�ڵ�G�������߶�GF��GC�к�������ϵ����֤����Ľ��ۣ�

��2�����̽����
��ͼ������1���еľ���ABCD��Ϊƽ���ı��Σ������������䣬��1���еĽ����Ƿ���Ȼ��������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪ƽ���ı���ABCD����A������Ϊ��2��6������B��y���ϣ���AD��BC��x�ᣬ��B��C��D�����������y=ax2+bx+c��a��0���Ķ�������Ϊ��2��2������F��m��6�����߶�AD��һ���㣬ֱ��OF��BC�ڵ�E��
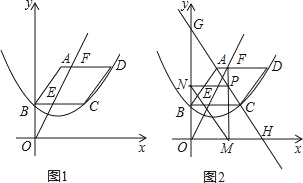
��1���������ߵı���ʽ��
��2�����ı���ABEF�����ΪS�������S��m�ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��
��3����ͼ2������F��FM��x�ᣬ����ΪM����ֱ��AC��P������P��PN��y�ᣬ����ΪN������MN��ֱ��AC�ֱ�x�ᣬy���ڵ�H��G�������߶�MN����Сֵ����ֱ��д����ʱm��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AD�ǡ�BAC��ƽ���ߣ�AD�Ĵ���ƽ���߽�AB�ڵ�F����BC���ӳ����ڵ�E������AE��DF.
��֤����1����EAD=��EDA����2��DF//AC����3����EAC=��B.
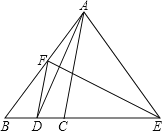
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ճ������һ��ɱ�Ϊ10Ԫ/���Ĺ���ƷͶ���г�����������
�������飬�õ��������ݣ�
���۵���x��Ԫ/���� | �� | 20 | 30 | 40 | 50 | 60 | �� |
ÿ��������y������ | �� | 500 | 400 | 300 | 200 | 100 | �� |
��1�����ϱ���x��y�ĸ����Ӧֵ��Ϊ������꣬�������ƽ��ֱ������ϵ�������Ӧ�ĵ㣬����y��x�ĺ�����ϵʽ�������������ϵʽ��
��2����۲��Ź涨���ù���Ʒ�����۵�����߲�����45Ԫ/���������۵���x��Ϊ����ʱ�����ճ������ù���Ʒÿ���õ�����8000Ԫ��������=�����ܼ۩��ɱ��ܼۣ�
��3�������۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ����������������Ƕ��٣�������=�����ܼ۩��ɱ��ܼۣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com