
����Ŀ��ij���ճ������һ��ɱ�Ϊ10Ԫ/���Ĺ���ƷͶ���г�����������
�������飬�õ��������ݣ�
���۵���x��Ԫ/���� | �� | 20 | 30 | 40 | 50 | 60 | �� |
ÿ��������y������ | �� | 500 | 400 | 300 | 200 | 100 | �� |
��1�����ϱ���x��y�ĸ����Ӧֵ��Ϊ������꣬�������ƽ��ֱ������ϵ�������Ӧ�ĵ㣬����y��x�ĺ�����ϵʽ�������������ϵʽ��
��2����۲��Ź涨���ù���Ʒ�����۵�����߲�����45Ԫ/���������۵���x��Ϊ����ʱ�����ճ������ù���Ʒÿ���õ�����8000Ԫ��������=�����ܼ۩��ɱ��ܼۣ�
��3�������۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ����������������Ƕ��٣�������=�����ܼ۩��ɱ��ܼۣ�

���𰸡���1��y=��10x+700����2�������۵���x��Ϊ30Ԫʱ�����ճ������ù���Ʒÿ���õ�����8000Ԫ����3����x=40ʱ��W�����ֵ9000
�������������������1��������㷨�ó�����λ�ã��������ô���ϵ������һ�κ�������ʽ���ɣ�
��2����������=�����ܼ�-�ɱ��ܼۻ�����������������=���������ó���ʽ������ɣ�
��3��������������������=��������W=��x-10����-10x+700�������ֵ���ɣ�
�����������1����ͼ����ͼ��

��ͼ�ɲ��룬y��x��һ�κ�����ϵ�������һ�κ���Ϊy=kx+b��k��0����
�����һ�κ�����ͼ����㣨20��500������30��400��
��![]() ��
��
��ã� ![]() ��
��
��һ�κ����Ĺ�ϵʽ�ǣ�y=-10x+700��
��2��������ɵã���x-10����-10x+700��=8000��
��ã�x=30��x=50������������ȥ��
�ʵ����۵���x��Ϊ30Ԫʱ�����ճ������ù���Ʒÿ���õ�����8000Ԫ��
��3���蹤�ճ������ù���Ʒÿ���õ�������WԪ��������ã�
W=��x-10����-10x+700��
=-10x2+800x-7000
=-10��x-40��2+9000
�ʵ�x=40ʱ��W�����ֵ9000��


 ��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��Rt��ABC��,��C=90,AC=6,BC=8,����P�ӵ�A��ʼ,�ر�AC���C��ÿ��1����λ���ȵ��ٶ��˶�,����D�ӵ�A��ʼ,�ر�AB���B��ÿ��![]() ����λ���ȵ��ٶ��˶�,��ǡ����ʼ�ձ��������������ֱ��PD��AC,����Q�ӵ�C��ʼ,�ر�CB���B��ÿ��2����λ���ȵ��ٶ��˶�,����PQ.��P,D,Q�ֱ�ӵ�A,Cͬʱ����,������һ�㵽��˵�ʱ,��������Ҳ��ֹ֮ͣ�˶�,���˶�ʱ��Ϊt��(t��0).
����λ���ȵ��ٶ��˶�,��ǡ����ʼ�ձ��������������ֱ��PD��AC,����Q�ӵ�C��ʼ,�ر�CB���B��ÿ��2����λ���ȵ��ٶ��˶�,����PQ.��P,D,Q�ֱ�ӵ�A,Cͬʱ����,������һ�㵽��˵�ʱ,��������Ҳ��ֹ֮ͣ�˶�,���˶�ʱ��Ϊt��(t��0).
(1)��tΪ��ֵʱ,�ı���BQPD�����Ϊ��ABC�����![]() ?
?
(2)�Ƿ����t��ֵ��ʹ�ı���PDBQΪƽ���ı���?�����ڣ����t��ֵ���������ڣ�˵�����ɣ�
(3)�Ƿ����t��ֵ,ʹ�ı���PDBQΪ����?������,���t��ֵ;��������,˵������,��̽����θı��Q���ٶ�(�����˶�)��ʹ�ı���PDBQ��ijһʱ��Ϊ���Σ����Q���ٶȡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
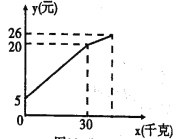
����Ŀ��һũ���������ǧ���Բ����ܲ����dz��ۣ�Ϊ�˷��㣬������һЩ��Ǯ���ã����г����۳�һЩ���ֽ��۳��ۣ��۳��ܲ�ǧ�����������г��е�Ǯ������������Ǯ���Ĺ�ϵ��ͼ��ʾ�����ͼ��ش��������⣺
��1������ǰ��ÿǧ���ܲ����۵ļ۸��Ƕ��٣�
��2�����ۺ�����ÿǧ��0.4Ԫ��ʣ���ܲ����꣬��ʱ�����е�Ǯ����������Ǯ����26Ԫ������һ�����˶���ǧ���ܲ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����㣺![]() ��2�����㣺
��2�����㣺![]()
��3���ⷽ�̣�![]()
��4���ⲻ��ʽ�� ���������ǵĽ⼯�������ϱ�ʾ����.
���������ǵĽ⼯�������ϱ�ʾ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������Ϊ�˽ⱾУ���꼶ѧ����1������������Ŀ��ѵ������������ȡ���꼶n��ѧ��������һ�β��ԣ��������Գɼ��ֳ����ࣺ���㡢���á������������ͳ�ƣ�����ͳ�ƽ�����Ƴ�����������������ͳ��ͼ.
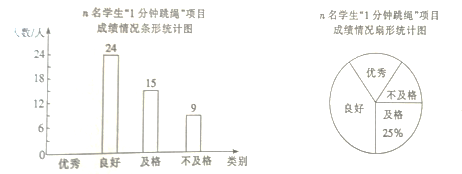
�����ͼ����Ϣ������������⣺
��1����n��ֵ.
��2��������ͳ��ͼ��������.
��3�����Ƹ�У���꼶800��ѧ���С�1������������Ŀ�ɼ�Ϊ�������ѧ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
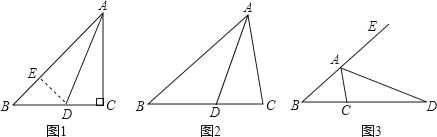
����Ŀ������ABC�У���ACB=2��B����ͼ��������C=90�㣬ADΪ��BAC�Ľ�ƽ����ʱ����AB�Ͻ�ȡAE=AC������DE����֤AB=AC+CD��
��1����ͼ��������C��90�㣬ADΪ��BAC�Ľ�ƽ����ʱ���߶�AB��AC��CD����������������ϵ������Ҫ֤������ֱ��д����IJ��룺
��2����ͼ������ADΪ��ABC�����ƽ����ʱ���߶�AB��AC��CD����������������ϵ����д����IJ��룬������IJ������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����о��С���ʮ�߽���Сѧ���鷨��������Ʒ��������֪ÿ��������Ʒ�ɼ���Ϊ![]() ����ί���1000���鷨��Ʒ�������ȡ�˲��ֲ�����Ʒ��ͳ�������ǵijɼ��������Ƴ�����ͳ��ͼ����
����ί���1000���鷨��Ʒ�������ȡ�˲��ֲ�����Ʒ��ͳ�������ǵijɼ��������Ƴ�����ͳ��ͼ����
������ | Ƶ�� | �ٷֱ� |
| 38 | 0.38 |
| ________ | 0.32 |
| ________ | ________ |
| 10 | 0.1 |
�ϼ� | ________ | 1 |

����������Ϣ������������⣺
��1������鷨��Ʒ�����ɼ��ĵ����Dz���_____����ղ顱�������顱����������_____��
��2������ϱ�������ȫ�鷨��Ʒ�����ɼ�Ƶ��ֱ��ͼ��
��3����80�֣���80�֣����ϵ��鷨��Ʒ������Ϊ�ȼ������Թ���ȫ�л�õȼ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��OΪ����ԭ�㣬�ı���OABCΪ���Σ�A��10��0����C��0��4������D��OA���е㣬��P�ڱ�BC����ÿ��1����λ�����ٶ��ɵ�C���B�˶���
��1����tΪ��ֵʱ���ı���PODB��ƽ���ı��Σ�
��2����OPDΪ����������ʱ��д����P�����꣨��ֱ��д���𰸣�����д���̣���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪:��2��A�ͳ���1��B�ͳ���������һ�ο��˻�11�֣���1��A�ͳ���2��B�ͳ���������һ�ο��˻�13��.����������Ϣ, ����������⣺
(1)1��A�ͳ���l��B�ͳ�����������һ�οɷֱ��˻����ٶ�?
(2)ij������˾����31�ֻ���ƻ�ͬʱ����A�ͳ�![]() ����B�ͳ�
����B�ͳ�![]() ����һ�����꣬��ǡ��ÿ�����������������ú���
����һ�����꣬��ǡ��ÿ�����������������ú���![]() ��ʽ�ӱ�ʾ
��ʽ�ӱ�ʾ![]() �������������˾��������;
�������������˾��������;
(3)��(2)�������£���A�ͳ�ÿ�������500Ԫ/�Σ�B�ͳ�ÿ�������600Ԫ/��.��ѡ����ʡǮ�����������������������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com