
| 3 |
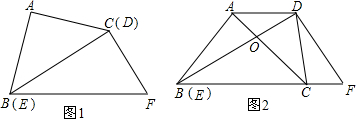
| 3 |
| DF |
| BD |
| ||
| 3 |
| 3 |
| 3 |
| AC |
| BC |
| AC |
| 6 |
| ||
| 2 |
| ||
| 2 |
| 2 |


科目:初中数学 来源: 题型:
 对11月份本社接待的外地游客来杭州旅游的首选景点作了一次抽样调查. 调查结果如下图表:
对11月份本社接待的外地游客来杭州旅游的首选景点作了一次抽样调查. 调查结果如下图表:| 景点 | 频数 | 频率 |
| 西湖 | 87 | 29% |
| 西溪湿地 | 75 | |
| 灵隐 | 21% | |
| 宋城 | 47 | 15.7% |
| 九溪 | 28 | 9.3% |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知△ABC中,AB=AC,∠A=36°.
如图,已知△ABC中,AB=AC,∠A=36°.查看答案和解析>>
科目:初中数学 来源: 题型:
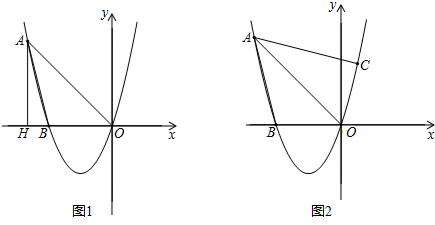
查看答案和解析>>
科目:初中数学 来源: 题型:
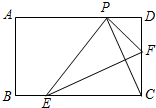 如图,在矩形纸片ABCD中,AB=3,BC=5,点E、F是BC、CD边上的动点(包括端点处),若将纸片沿EF折叠,使得点C恰好落在AD边上点P处.设CF=x,则x的取值范围为
如图,在矩形纸片ABCD中,AB=3,BC=5,点E、F是BC、CD边上的动点(包括端点处),若将纸片沿EF折叠,使得点C恰好落在AD边上点P处.设CF=x,则x的取值范围为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com