
分析 根据平均数,方差的公式进行计算.
解答 解:平均数$\overline{x′}$′=$\frac{1}{5}$(x1+1+x2+1+x3+1+x4+1+x5+1)=$\overline{x}$+1,
方差s′2=$\frac{1}{5}$[(x1+1-$\overline{x}$-1)2+(x2+1-$\overline{x}$-1)2+…+(x5+1-$\overline{x}$-1)2]
=$\frac{1}{5}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(x5-$\overline{x}$)2]
=s2,
故答案为:$\overline{x}$+1,s2.
点评 本题考查了平均数、方差的计算.关键是熟悉计算公式,会将所求式子变形,再整体代入.


科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{6}{x}$ | B. | y=$\frac{x}{6}$ | C. | y=x2 | D. | y=$\frac{x+1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
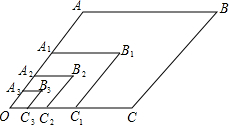 如图,在菱形OABC中,∠AOC=60°,OA=2$\sqrt{2}$,以点O为位似中心,相似比为$\frac{1}{2}$,将菱形OABC缩小,得到菱形OA1B1C1;再以点O为位似中心,相似比为$\frac{1}{2}$,将菱形OA1B1C1缩小,得到菱形OA2B2C2;…,以此类推,则菱形OA2016B2016C2016的面积为$\sqrt{6}$×($\frac{1}{2}$)4032.
如图,在菱形OABC中,∠AOC=60°,OA=2$\sqrt{2}$,以点O为位似中心,相似比为$\frac{1}{2}$,将菱形OABC缩小,得到菱形OA1B1C1;再以点O为位似中心,相似比为$\frac{1}{2}$,将菱形OA1B1C1缩小,得到菱形OA2B2C2;…,以此类推,则菱形OA2016B2016C2016的面积为$\sqrt{6}$×($\frac{1}{2}$)4032.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
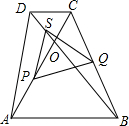 如图,在等腰梯形ABCD中,AB∥DC,AD=BC,对角线AC与BD相交于点O,∠ACD=60°,点S、P、Q分别为OD、OA、BC的中点.
如图,在等腰梯形ABCD中,AB∥DC,AD=BC,对角线AC与BD相交于点O,∠ACD=60°,点S、P、Q分别为OD、OA、BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
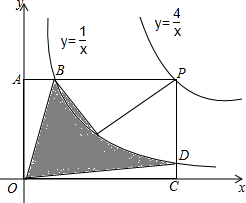 如图,点P为反比例函数y=$\frac{4}{x}$(x>0)图象上一点,过点P作y轴的垂线,交双曲线y=$\frac{1}{x}$于点B,交y轴于点A,过点P作x轴的垂线,交双曲线y=$\frac{1}{x}$于点D,交x轴于点C,连接OP交双曲线y=$\frac{1}{x}$于点E,则连接BO,OD,DE,EB而围成的阴影部分面积为( )
如图,点P为反比例函数y=$\frac{4}{x}$(x>0)图象上一点,过点P作y轴的垂线,交双曲线y=$\frac{1}{x}$于点B,交y轴于点A,过点P作x轴的垂线,交双曲线y=$\frac{1}{x}$于点D,交x轴于点C,连接OP交双曲线y=$\frac{1}{x}$于点E,则连接BO,OD,DE,EB而围成的阴影部分面积为( )| A. | 1 | B. | $\frac{5}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com