
如图1,矩形ABCD的边AD在y轴上,抛物线y=x2﹣4x+3经过点A、点B,与x轴交于点E、点F,且其顶点M在CD上.
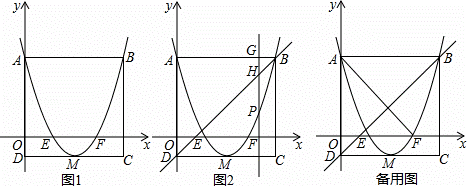
(1)请直接写出下列各点的坐标:A () ,B ( , ) ,C ( , ) ,D ( , ) ;
(2)若点P是抛物线上一动点(点P不与点A、点B重合),过点P作y轴的平行线l与直线AB交于点G,与直线BD交于点H,如图2.
①当线段PH=2GH时,求点P的坐标;
②当点P在直线BD下方时,点K在直线BD上,且满足△KPH∽△AEF,求△KPH面积的最大值.
解:(1)A(0,3),B(4,3),C(4,﹣1),D(0,﹣1).
(2)①设直线BD的解析式为y=kx+b(k≠0),由于直线BD经过D(0,﹣1),B(4,3),
∴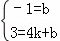 ,
,
解得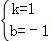 ,
,
∴直线BD的解析式为y=x﹣1.(5分)
设点P的坐标为(x,x2﹣4x+3),则点H(x,x﹣1),点G(x,3).
1°当x≥1且x≠4时,点G在PH的延长线上,如图①.
∵PH=2GH,
∴(x﹣1)﹣(x2﹣4x+3)=2[3﹣(x﹣1)],
∴x2﹣7x+12=0,
解得x1=3,x2=4.
当x2=4时,点P,H,G重合于点B,舍去.
∴x=3.
∴此时点P的坐标为(3,0).
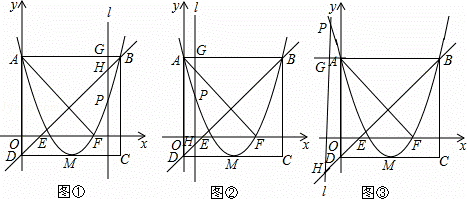
2°当0<x<1时,点G在PH的反向延长线上,如图②,PH=2GH不成立.
3°当x<0时,点G在线段PH上,如图③.
∵PH=2GH,
∴(x2﹣4x+3)﹣(x﹣1)=2[3﹣(x﹣1)],
∴x2﹣3x﹣4=0,解得x1=﹣1,x2=4(舍去),
∴x=﹣1.此时点P的坐标为(﹣1,8).
综上所述可知,点P的坐标为(3,0)或(﹣1,8).
②如图④,令x2﹣4x+3=0,得x1=1,x2=3,
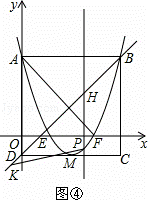
∴E(1,0),F(3,0),
∴EF=2.
∴S△AEF=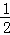 EF•OA=3.
EF•OA=3.
∵△KPH∽△AEF,
∴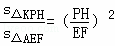 ,
,
∴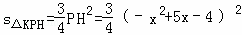 .
.
∵1<x<4,
∴当 时,s△KPH的最大值为
时,s△KPH的最大值为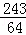 .
.
故答案为:(0,3),(4,3),(4,﹣1),(0,﹣1).


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
下列命题错误的是( )
|
| A. | 所有的实数都可用数轴上的点表示 | B. | 等角的补角相等 |
|
| C. | 无理数包括正无理数,0,负无理数 | D. | 两点之间,线段最短 |
查看答案和解析>>
科目:初中数学 来源: 题型:
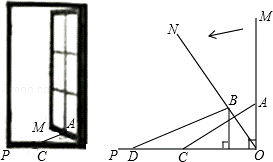
如图,一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在OP上滑动,将窗户OM按图示方向想内旋转35°到达ON位置,此时,点A、C的对应位置分别是点B、D.测量出∠ODB为25°,点D到点O的距离为30cm.
(1)求B点到OP的距离;
(2)求滑动支架的长.
(结果精确到1cm.参考数据:sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
查看答案和解析>>
科目:初中数学 来源: 题型:
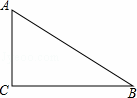
如图,在Rt△ABC中,∠ACB=90°.
(1)先作∠ABC的平分线交AC边于点O,再以点O为圆心,OC为半径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);
(2)请你判断(1)中AB与⊙O的位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )

|
| A. | 45° | B. | 54° | C. | 40° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:
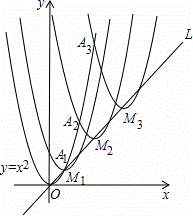
如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:
①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;
②抛物线依次经过点A1,A2,A3…An,….则顶点M2014的坐标为( ,____).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com